|
En física atómica, molecular y óptica, así como en química cuántica, Hamiltoniano molecular es el nombre dado al operador Hamiltoniano que representa la energía del sistema constituido por los electrones y el núcleo de una molécula. Este es una operador auto-adjunto, es decir Hermitiano, cuya ecuación de Schrödinger asociada juega un papel central en la química computacional y en la física computacional para calcular propiedades de moléculas y agredados de las mismas, así como la conductividad óptica, propiedades magnéticas y reactividad
Conocimientos adicionales recomendados
IntroducciónLos ladrillos de una molécula son los núcleos atómicos mientras que su argamasa son los electrones. Los primeros están definidos por su número atómico Z; mientras que los segundos por la carga elemental negativa q. La carga de una núcleo es Zq positiva. Los electrones y nucleos son, de una manera muy aproximada, cargas puntuales y partículas puntuales. El Hamiltoniano molecular es es la suma de varios términos: los términos mayores son la energía cinética de los electrones y las interacciones coulombianas entre los dos tipos de partículas cargadas. A esta parte del Hamiltoniano molecular se le conoce como Hamiltoniano de Coulomb. A este último hay que agregarle muchos términos de pequeña magnitud, la mayoría de ellos debidos a los espines electrónicos y nucleares. A pesar de que es generalmente aceptado que la solución de la ecuación de Schrödinger independiente del tiempo asociada al Hamiltoniano de Coulomb de una molécula predecirá la mayor parte de las propiedades de la misma, incluyendo su estructura tidimensional, los cálculos basados en el Hamiltoniano de Coulomb son escasos. La principal razón de lo anterior es que la ecuación de Schrödinger es muy difícil de resolver. Las aplicaciones prácticas de dicha ecuación se restringen a sistemas muy simples como la molécula de hidrógeno. Casi todos los cálculos de funciones de onda de moléculas están basados en la separación del Hamiltoniano de Coulomb que fue divisada primeramente por Max Born y Oppenheimer; a dicha simplificación se le conoce como aproximación de Born-Oppenheimer. En dicha aproximación, los términos de energía cinética de los núcleos son omitidos del Hamiltoniano de Coulomb y se considera al Hamiltoniano remanente como únicamente el Hamiltoniano de los electrones. El núcleo estacionario se considera en el análisis únicamente como el generador del potencial eléctrico dentro del que se mueven los electrones, dentro del marco de la mecánica cuántica. Con esta perspectiva el Hamiltoniano molecular ha sido reducido a lo que se conoce como Hamiltoniano de núlceo afianzado ("clamped nucleus Hamiltonian"), que se encuentra expresado únicamente en términos de funciones de las coordenadas electrónicas. Una vez que se resuelve la ecuación de Schrödinger asociada al Hamiltoniano de núcleo afianzado para un número suficiente de constelaciones del núcleo, un eigenvalor apropiado, usualmente el más bajo, puede ser visto como una función de de las coordenadas del núcleo, que corresponde a una superficie de energía potencial. En cálculos prácticos, la superficie es usualmente expresada en términos de alguna función analítica. En el segundo paso de la aproximación de Born-Oppenheimer la parte del Hamiltoniano de Coulomb completo que depende de los electrones es reemplazada por la superficie de energía potencial. Esto convierte el Hamiltoniano molecular total en un Hamiltoniano que solo actua en las coordenadas nucleares. En el caso se que se de una singularidad en la aproximación de Born-Oppenheimer, lo que ocurre cuando las energías de diferentes estados electrónicos son cercanas; es necesario conocer el potencial de las superficies de frontera. La ecuación de Schrödinger del movimiento nuclear puede ser resuelta para un referencial fijo (el laboratorio), pero no se encuentran representadas las energía debida a las translaciones y rotaciones de los núcleos. Sola las vibraciones internas de las moléculas entran en el problema. Sin embargo, para moléculas mayores que las triatómicas, es común introducir la aproximación armónica, la cual estima la superfice de potencial como una función cuadrática de los desplazamientos atómicos. Haciendi esta aproximación, podemos convertir el Hamiltoniano en una suma suma de Hamiltonianos de osciladores armónicos lineales no acoplados. El oscilador armónico lineal es uno de los pocos sistemas para los que se conocen soluciones exactas de la ecuación de Schrödinger.
Hamiltoniano de CoulombLa forma algebraica de los operadores correspendientes a muchos observables pueden obtenerse mediante las regla de la cuantización canónica:
Clásicamente, los electrones y núcleos de una molécula tienen una energía cinética que puede representarse como p2/(2m) e interaccionan mediante fuerzas electrostáticas, las cuales decrecen proporcionalmente con el inverso del cuadrado de la distancia en el espacio euclidiano entre las pártículas cargadas. Sean las partículas cargadas i y j y vector euclidiano que representa la distancia entre ellas r. Tenemos que:
Mediante la cuantización de la energía clásica del Hamiltoniano se obtiene el operador hamiltoniano de la molécula, que siempre es llamado Hamiltoniano de Coulomb. Este Hamiltoniano es la suma de cinco términos. Estos son:
Ver: potencial eléctrico Aquí, Mi es la masa del núcleo i-ésimo, Zi es el número atómico del núcleo i-ésimo y me es la masa del electrón. El operador lapaciano de la partícula i-ésima es: Debido a que el operador de energía cinética es un producto interno, es invariante bajo la rotación del referencial cartesiano respecto del cual se mide, donde xi, yi, y zi son expresadas. Sin embargo, el operador de energía cinética, de cualquier forma, no es invariante ante la traslación del referencial. Ecuación de Schrödinger del Hamiltoniano de CoulombEl Hamiltoniano de Coulomb tiene un espectro continuo debido al movimiento del centro de masas de la molécula en un espacio homogéneo. En mecánica clásica es fácil separar el movimiento del centro de masas de un sistema de partículas del movimiento de cada una de las partículas individuales de dicho sistema. Clásicamente, el moviento del centro de masa está desacoplado de los movimientos de las partículas individuales. El centro de masas se mueve uniformemente a través del espacio como si se tratara de una partícula puntual cuya masa sea igual a la suma Mtot de las masas de todas las partículas individuales. En mecánica Cuántica una partícula libre tiene como función de estado una función de onda plana, la cual es una función no cuadrático integrable de momento bien definido. La energía cinética de esta partícula tiene un valor dentro de En la mecánica cuántica separar el movimiento del
CM es más complicado que en la mecánica clásica. Introduciendo el vector de coordenadas El primer término de H es la energía cinética del centro de masa, la cual puede ser analizada separadamente debido a que H' no depende de Actualmente, no existen muchas aplicaiones de H'. Sin embargo, el trabajo pionero de Kołos y Wolniewicz[1] sobre la molécula de hidrógeno nos da una aplicación temprana. En la mayoria de los cálculos de funciones de onda moleculares el problema de los electrones es resuelto utilizando el hamiltoniano de núcleo afianzado en el primer paso de la aproximación de Born-Oppenheimer. Vea la ref.[2] para una discusión profunda de las propiedades matemáticas del Hamiltoniano de Coulomb. En dicho artículo también se discute que si uno puede tomar a "a priori" el concepto de una molécula (entendiendo molécula como un sistema estable de electrones y núcleos con una geometria bien definida) solamente de las propiedades del Hamiltoniano de Coulomb. Hamiltoniano de Núcleo afianzadoEl hamiltoniano de núcelo afianzado describe la energía de los electrones en el campo electrostático del núcleo atómico, el cual se asume como estacionario con respecto de un referencial inercial. La forma del hamiltoniano electrónico es: Las coordenadas de los electrones y el núcleo están expresadas con respecto a un referencial que está fijo a este último, por lo que este permanece en reposo con respecto a dicho referencial. Este es un referencial inercial porque se asume que no hay fuerzas o torques externos actuando sobre el núcleo, por lo cual no experimenta ninguna aceleración lineal ni angular. La posición del origen del sistema de coordenadas de este referencial es arbitraria. Usualmente es posicionado en un núcleo central, o en centro de masa de la molécula. Algunas veces se afirma que el núcleo está "en reposo con respecto a un referencial fijo en el espacio". Esta afrimación implica que se ve al núcleo como una partícula clásica, porque una partícula no puede estar en reposo desde el punto de vista de la mecánica cuántica. Esto se debe a que una partícula en reposo tendría un momento lineal bien defininido (cero) así como una posición ígualmente bien definida, lo cual entraría en contradicción con el principio de incertidumbre de Heisenberg.
Un número suficiente de soluciones de la ecuación de Schrödinger de Hel conduce a una superficie de energía potencial
Para:
Donde t y s son vectores arbitrarios y Δφ es un ángulo infinitesimal, Δφ >> Δφ2. La condición de invarianza de la superficie de energía potencial se cumple completamente cuando dicha superficie de energía potencial es expresada en términos de diferencias de, y ángulos entre Ri, el cual es usualmente el caso. Hamiltoniano de Movimento Nuclear ArmónicoEn la parte restante del artículo se considerará que la molécula es semi-rígida. En el segundo paso de la aproximación de Borhn-Oppenheimer la energía cinética del núcleo Tn es reintroducida y consideramos a la ecuación de Schrödinger con el Hamiltoniano: : Uno puede reconocer varios términos en esta solución: el movimiento del centro de masa del núcleo (3 grados de libertad), la rotación total de la molécula (3 grados de libertad) y las vibraciones del núcleo. En general, esto no es posible con con la energía cinética del núcleo dada, porque no se puede separar explicitamente los 6 grados externos de libertad respecto de los 3N-6 grados internos de libertad. De hecho, el operador de energía cinética es definido con respecto al referencial fiho al espacio. Si nosotros movemos el origen del referencial fijo al espacio al del referencial fijo al centro de masa de la molécula, aplicando la regla de la cadena, aparece el término de polarización de masa. Hamiltoniano del movimiento nuclear de WatsonReferencias
Véase también
Categoría: Química cuántica |
|
| Este articulo se basa en el articulo Hamiltoniano_molecular publicado en la enciclopedia libre de Wikipedia. El contenido está disponible bajo los términos de la Licencia de GNU Free Documentation License. Véase también en Wikipedia para obtener una lista de autores. |


Enciclopedia




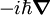 e interprete a q como un operador multiplicativo. Aquí
e interprete a q como un operador multiplicativo. Aquí  es el operador nabla. Las bien conocidas reglas de conmutación para los operadores p y q se deducen directamente de las reglas de diferenciación.
es el operador nabla. Las bien conocidas reglas de conmutación para los operadores p y q se deducen directamente de las reglas de diferenciación.
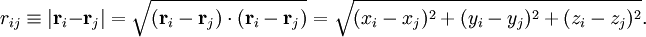
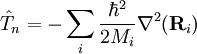
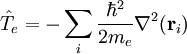
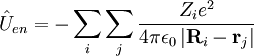
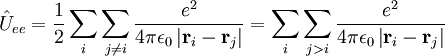
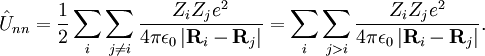
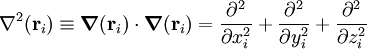 .
.
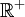 . El CM tiene una cierta probalidad de hallarse en cualquier región del espacio. Esto obedece al
. El CM tiene una cierta probalidad de hallarse en cualquier región del espacio. Esto obedece al  del centro de masa con tres de los grados de libertad dek sistema y eliminado el vector de coordenadas de una partícula arbitrariamente, de tal modo que el número de de grados de libertad del sistema permaenzca constante, podemos obtener mediante una transformación lineal un nuevo conjunto de coordenadas ti. Estas coordenas son una combinación lineal de las anteriores coordenadas de "todas" las partículas (
del centro de masa con tres de los grados de libertad dek sistema y eliminado el vector de coordenadas de una partícula arbitrariamente, de tal modo que el número de de grados de libertad del sistema permaenzca constante, podemos obtener mediante una transformación lineal un nuevo conjunto de coordenadas ti. Estas coordenas son una combinación lineal de las anteriores coordenadas de "todas" las partículas (
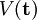 consiste en los términos de Coulomb expresados en las nuevas coordenadas. El nuevo término de
consiste en los términos de Coulomb expresados en las nuevas coordenadas. El nuevo término de 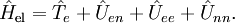
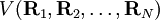 . Se asume que la dependencia funcional de V respecto de sus coordenadas es tal que:
. Se asume que la dependencia funcional de V respecto de sus coordenadas es tal que:
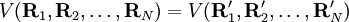
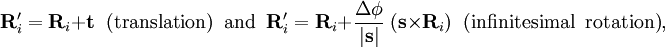
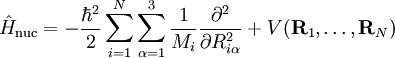 .
.
