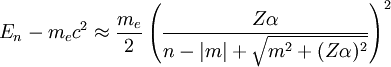|
Los átomos hidrogenoides son átomos formados por un núcleo y un solo electrón. Se llaman así porque su comportamiento químico es similar al del hidrógeno. Es hidrogenoide pues cualquiera de los isótopos del hidrógeno, claro está. Un caso típico de átomo hidrogenoide es también el de un átomo de cualquier elemento que se ha ionizado hasta perder todos los electrones menos uno. Existen además multitud de átomos exóticos que también tienen un comportamiento hidrogenoide por motivos diversos. Conocimientos adicionales recomendados
IntroducciónComo en el caso del átomo de hidrógeno los átomos hidrogenoides son uno de los pocos problemas mecánico cuánticos que se pueden resolver de forma exacta. Los átomos o iones cuya capa de valencia está constituida por un único electrón (por ejemplo en los metales alcalinos) tienen propiedades espectroscópicas y de enlace semejantes a las de los átomos hidrogenoides. La configuración electrónica más simple posible es la de un único electrón. La resolución analítica del átomo de hidrógeno neutro que posee la misma cantidad de electrones, es decir uno, es en esencia la misma para los átomos hidrogenoides. Así pues la forma de los orbitales y los niveles de energía serán semejantes. Por el contrario, para átomos con dos o más electrones la resolución de las ecuaciones solo se puede hacer mediante métodos aproximativos. Los orbitales de átomos multielectrónicos son cualitativamente similares a los orbitales del hidrógeno y, en los modelos atómicos más simples, se considera que tienen la misma forma. Pero si se pretende realizar un cálculo riguroso y preciso se tendrá que recurrir a aproximaciones numéricas. Los orbitales de los átomos hidrogenoides se identifican mediante tres números cuánticos: n, l, y ml. Las reglas que restringen los valores de los números cuánticos y sus energías (ver más abajo) explican la configuración electrónica de los átomos y la conformación de la tabla periódica. Los estados estacionarios (estados cuánticos) de los átomos hidrogenoides son sus orbitales atómicos. A pesar de todo, en general, el comportamiento de un electrón no está plenamente descrito por un orbital simple. Los estados electrónicos se representan mejor como "mezclas" dependientes del tiempo (combinaciones lineales) de varios orbitales. Ver Orbitales moleculares por combinación lineal de orbitales atómicos. El número cuántico n apareció por primera vez en el modelo atómico de Bohr. Determina, entre otras cosas, la distancia de los electrones con respecto al núcleo. Todos los electrones con el mismo valor de n forman un nivel o capa. Los electrones con idéntico número n pero diferente l componen los llamados subniveles o subcapas. El modelo atómico de Sommerfeld que incorporaba un refinamiento relativista del electrón probó que la energía dependía también de los otros números cuánticos tal como se aprecia en la solución relativista mediante la ecuación de Dirac. Caracterización matemáticaLa caracterización de los átomos hidrogenoides se realiza en el marco de la mecánica cuántica, ya que debido al tamaño de esos sistemas físicas ni la mecánica clásica que describe adecuadamente el movimiento de partículas macroscópicas a velocidades moderadas, ni el electromagnetismo clásico son aplicables a escalas tan pequeñas. Dentro de la mecánica cuántica una primera aproximación se obtiene mediante la ecuación de Schrödinger que predice cualitativamente todas las características importantes de un estado de equilibrio de un átomo hidrogenoide y da valores cuantitativos muy aproximados para casi todas las magnitudes. Un refinamiento de este tratatamiento es el análisis relativista mediante la ecuación de Dirac que predice pequeñas correcciones a las soluciones obtenidas del análisis no-relativista mediante la ecuación de Schrödinger.
Potencial electrostáticoLos orbitales atómicos de los átomos hidrogenoides son las soluciones de la ecuación de Schrödinger para el caso de un potencial de simetría esférica. En este caso, el término de potencial es el potencial de la ley de Coulomb: donde
Función de onda no relativistaDebido a que el potencial tiene simetría esférica es posible separar el movimiento del centro de masas del movimiento relativo entre electrón y núcleo. Así, el movimiento relativo se puede tratar como el movimiento de una partícula cuya masa es la masa reducida, μ, del sistema. De esta manera, la función de onda es una función de sólo tres variables espaciales. Tras eliminar la dependencia temporal, la ecuación de Schrödinger es una ecuación en derivadas parciales de tres variables.Debido a que el potencial tiene simetría esférica es conveniente utilizar las coordenadas esféricas para obtener las soluciones, aplicando para ello el método de separación de variables. De esta forma cualquier autofunción ψ puede escribirse como un producto de tres funciones que suelen escribirse de la forma siguiente: donde θ representa el ángulo polar (colatitud) y φ el ángulo azimutal. Esta función de onda deberá estar además normalizada a 1 por lo que se añadirá una constante de normalización. El resto de la ecuación se separa entre la parte radial representada por la función radial que incorporará la constante de normalización y la angular representada por los armónicos esféricos. Todas estas funciones serán dependientes de los tres números cuánticos antes citados, n, l y m. Así, se tiene lo siguiente: Los números cuánticos no son independientes unos de otros por lo que el número de combinaciones posibles de estas funciones está limitado. Las restricciones son las siguientes: La función radial ya normalizada se representa como: Siendo Sin embargo, es más habitual encontrar las autonfunciones expresadas en función de la función radial reducida: Así pues la función de onda queda como sigue: Niveles de energía no relativistaEn el caso de los átomos hidrogenoides al no haber interacciones entre electrones, pues solo hay uno, la energía de los orbitales atómicos puede ser calculada analíticamente de forma exacta. Los valores de energía permitidos son
Habitualmente se considera 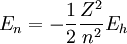 Donde Función de onda relativistaLa ecuación de Schrödinger aplicada a electrones es sólo una aproximación no relativista a la ecuación de Dirac que da cuenta tanto del efecto del spin del electrón. En el tratamiendo de Dirac de los electrones de hecho la función de onda debe substituirse por un espinor de cuatro componentes: Donde las funciones F y G se expresan en términos de funciones hipergeométricas: A modo de comparación con el caso no relativista se dan a continuación la forma explícita del espinor de funciones de onda del estado fundamental: El límite no relativista se obtiene haciendo tender Niveles de energía relativistaEl tratamiento de los electrones mediante la ecuación de Dirac sólo supone pequeñas correcciones a los niveles dados por la ecuación de Schrödinger. Tal vez el efecto más interesante es la desaparición de la degeneración de los niveles, por el efecto de la interacción espín-órbita consistente en que los electrones con valores diferentes del tercer número cuántico m (número cuántico magnético) tienen diferentes energía debido al efecto sobre ellos del momento magnético del núcleo atómico. De hecho los niveles energéticos vienen dados por:[1] Donde:
Si se prescinde de la energía asociada a la masa en reposo del electrón estos niveles pueden resultan cercanos a los predichos por la ecuación de Schrödinger, especialmente en el caso m = 0: ReferenciaNotas
BibliografíaVéase también |
|
| Este articulo se basa en el articulo Átomo_hidrogenoide publicado en la enciclopedia libre de Wikipedia. El contenido está disponible bajo los términos de la Licencia de GNU Free Documentation License. Véase también en Wikipedia para obtener una lista de autores. |


Enciclopedia




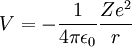
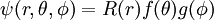
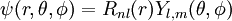
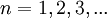
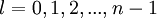
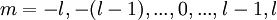
![R_{nl}(r) = - \left [ \frac{(n-l-1)!}{2n[(n+l)!]^3} \right ]^{1/2} \left ( \frac{2Z}{na_\mu} \right )^{l+3/2}r^{l}e^{-\frac{Zr}{na_\mu}}L_{n+l}^{2l+1} \left(\frac{2Zr}{na_\mu} \right )](images/math/3/a/c/3acd16213d69ab0d2d4ea75e34b5296b.png)
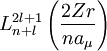 las funciones asociadas de Laguerre y
las funciones asociadas de Laguerre y 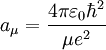 . Nótese que
. Nótese que 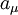 es aproximadamente igual al
es aproximadamente igual al 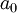 . Si la masa del núcleo es infinita entonces
. Si la masa del núcleo es infinita entonces 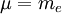 y
y 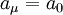 .
.
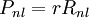
![\psi_{nlm}(\theta,\phi,r)=\frac{P_{nl}(r)}{r}Y_{l,m}(\theta, \phi )= - \left [ \frac{(n-l-1)!}{2n[(n+l)!]^3} \right ]^{1/2} \left ( \frac{2Z}{na_\mu} \right )^{l+3/2}r^{l+1}e^{-\frac{Zr}{na_\mu}}L_{n+l}^{2l+1} \left(\frac{2Zr}{na_\mu} \right )Y_{l,m}(\theta, \phi )](images/math/4/e/9/4e958275bcaaa6425a237a746394ddfe.png)
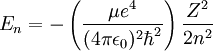 .
.
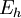 es la
es la 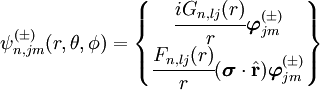
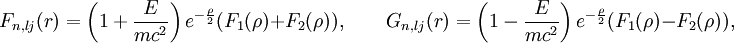
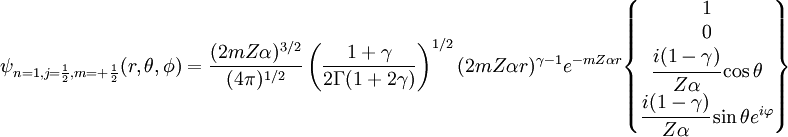
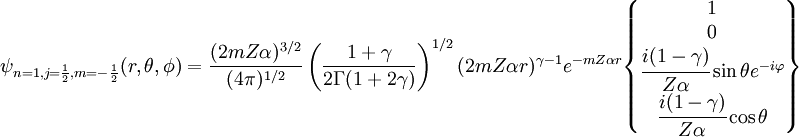
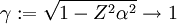 , es decir, haciendo tender la constante de estructura fina a cero.
, es decir, haciendo tender la constante de estructura fina a cero.
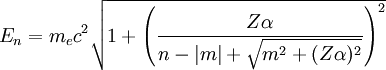
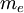 , es la masa del
, es la masa del 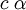 , son la
, son la 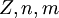 , son el número de protones del núcleo, el número cuántico principal y el número cuántico magnético.
, son el número de protones del núcleo, el número cuántico principal y el número cuántico magnético.