|
Un campo de Yang-Mills es un tipo campo físico usado sobre todo en teoría cuántica de campos cuyo lagrangiano tiene la propiedad de ser invariante bajo una transformación de gauge local. Producto destacado
HistoriaEn 1954, Yang y Mills[1] sugierieron que el principio de invariancia local de fase o invariancia de gauge local no eran compatibles con una teoría de campos local, es decir, que obedeciera los principios relativistas de causalidad. Es decir cuando, como es común, el lagrangiano de un campo tiene alguna simetría interna dada por un grupo de transformaciones de gauge, debería ser posible escoger en cada punto del espacio una transformación de gauge diferente, sin que eso hiciese que las ecuaciones de la teoría fueran alteradas. Así Yang y Mills buscaron la teoría más general de lagrangiano para un campo con invariancia de gauge local. De hecho la electrodinámica cuántica era ya una teoría con invariancia de gauge local, donde el grupo de gauge era precisamente el grupo de Lie U(1). El resultado del trabajo de Yang y Mills fue una generalización del lagrangrangiano de la electrodinámica cuántica, donde ahora el grupo de gauge era un grupo no conmutativo. Formulación matemáticaPara construir un campo de Yang-Mills cuyo grupo de gauge (1) Bajo una transformación de gauge local (2) Donde:
Campos bosónicos de Yang-MillsLos campos de Yang-Mills propiamente dichos son m campos vectoriales o más propiamente 1-formas con valores sobre el álgebra de Lie asociada al grupo de gauge, cada campo bosónico j viene dado por: (3) Dada la ley de transformación () es sencillo ver que a partir de estas 1-formas puede definirse un operador diferencial o derivada covariante del campo definda como: (3) Donde g es un parámetro real llamado constante de acoplamiento. Es sencillo comprobar que se cumplen las leyes de transformación: (4) Para una transformación de gauge infinitesimal (5) Donde los coeficientes fijk son las constantes de estructura del álgebra de Lie: (6) Lagrangiano de un campo de Yang-Mills
Propiedades de un campo gauge
Véase tambiénReferencias
Categoría: Teoría cuántica de campos |
|
| Este articulo se basa en el articulo Campo_de_Yang-Mills publicado en la enciclopedia libre de Wikipedia. El contenido está disponible bajo los términos de la Licencia de GNU Free Documentation License. Véase también en Wikipedia para obtener una lista de autores. |


Enciclopedia




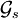 de dimensión m, necesitamos un campo multicomponente
de dimensión m, necesitamos un campo multicomponente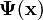 (cuyas componentes
(cuyas componentes 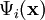 suelen ser espinores de Dirac). Todas las componentes del campo están definidas sobre un espacio-tiempo
suelen ser espinores de Dirac). Todas las componentes del campo están definidas sobre un espacio-tiempo 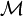 :
:
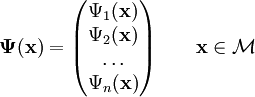
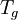 el campo se transformaría de acuerdo con:
el campo se transformaría de acuerdo con:
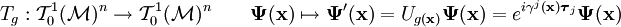
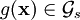 es el elemento del grupo de gauge asignado al punto
es el elemento del grupo de gauge asignado al punto 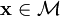 .
.
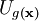 denota una matriz dada por una representación unitaria del grupo de gauge
denota una matriz dada por una representación unitaria del grupo de gauge 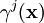 , son m funciones definidas sobre el espacio-tiempo que parametrizan la transformación local de gauge (diferentes elecciones de esas funciones representan diferentes transformaciones de gauge).
, son m funciones definidas sobre el espacio-tiempo que parametrizan la transformación local de gauge (diferentes elecciones de esas funciones representan diferentes transformaciones de gauge).
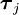 , es una base del álgebra de Lie
, es una base del álgebra de Lie 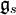 asociada al grupo de gauge
asociada al grupo de gauge 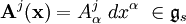

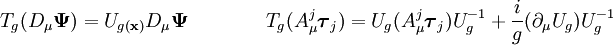
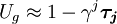 la última de las expresiones de (
la última de las expresiones de (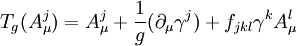
![[\boldsymbol{\tau}_i,\boldsymbol{\tau}_j] = f_{ijk}\boldsymbol{\tau}_k](images/math/5/7/d/57d063fda45afc57a1cf6037386cb41e.png)

