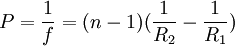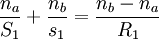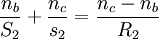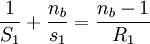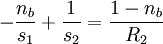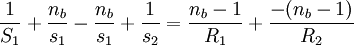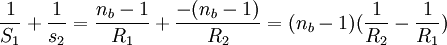Dioptría

Unidad que expresa con valores positivos o negativos el poder de refracción de una lente, y que equivale al valor recíproco o inverso de su longitud focal expresada en metros. El signo '+' (positivo) corresponde a los lentes convergentes, y el '-' (negativo) a los divergentes. Así, una lente cuya longitud focal sea de +1 metro, tendrá una potencia de 1 dioptría y una lente de +2 dioptrías es una lente convergente de longitud focal de 0,5 metros.

Conocimientos adicionales recomendados

Cómo realizar un pesaje correcto

Procedimientos normalizados de trabajo (PNT) para la comprobación de balanzas

Guía de técnicas básicas de medición en el laboratorio

Para una lente delgada, con dos radios de curvatura, la potencia en dioptrías puede calcularse a partir de la siguiente fórmula:

Donde,

P: Representa la potencia de la lente en dioptrías.

f: Longitud focal en metros.

n: Es el índice de refacción del material (por lo general el aire es = 1,003 y no ha sido tenido en cuenta en esta expresión).

R₁ y R₂: Denotan los radios de curvatura de la lente correspondiendo R₁ al lado izquierdo de la lente y R₂ al lado derecho siendo su signo determinado por el criterio general de signos en óptica: positivo si el centro de curvatura de la superficie reside a la derecha y negativo si el centro de curvatura se sitúa a la izquierda de la superficie.

Esta fórmula se deduce fácilmente a partir de la ecuación de un dioptrio, una superficie esférica refractora, aplicada sobre dos superficies y en la aproximación paraxial de ángulos pequeños.

Se tienen tres materiales con índices de refracción n_a, n_b, n_c separados por superficies esféricas. Tomamos n_a=1 al haber aire en un extremo de la lente y n_c=1 al haber aire en el otro extremo. La superficie de la lente tiene un radio exterior R₁ y radio interior R₂, donde el radio interior es mayor que exterior. Luego:

Aplicando n_a=1, n_c=1 y que s₁=-S₂ entonces:

Sumando estas dos ecuaciones nos queda:

Enlaces externos