|
El límite clásico es la habilidad de una teoría física para aproximarse al comportamiento predicho por la mecánica clásica cuando el valor de cierto parámetro especial de estas teorías se aproxima un "valor clásico". El límite clásico es usado en las teorías físicas que predicen un comportamiento no-clásico. Los casos más usuales de límite clásico son:
Producto destacado
Límite clásico de la mecánica cuánticaPara conciliar las predicciones de la mecánica cuántica a nivel microscópico con las predicciones de la mecánica clásica a nivel macroscópico, Niels Bohr introdujo el principio de correspondencia dentro de la teoría cuántica. Dicho principio postula algunos de los argumentos de continuidad deben ser aplicados al límite clásico de los sistemas cuánticos a medida que los valores de la constante de Planck se aproximan a cero. En la mecánica cuántica, debido al principio de incertidumbre de Heisenberg, un electrón no puede estar nunca en reposo; tiene siempre que tener una energía cinética distinta de cero, un resultado que no se encuentra en la mecánica clásica. Por ejemplo, si consideramos algo relativamente más grande que un electrón, tal como una pelota de fútbol, el principio de incertidumbre predice que no puede tener una energía cinética igual a cero, pero la incertidumbre en la energía cinética es tan pequeña, que la pelota de fútbol puede parecer que estuviese en reposo, y por esta razón parece obedecer a la mecánica clásica. En general, si grandes energías y grandes objetos (en comparación con el tamaño y los niveles de energía de un electrón) son considerados en la mecánica cuántica, los resultados parecerán obedecer a la mecánica clásica. De acuerdo con el principio de correspondencia de Bohr, todas las ecuaciones de la mecánica cuántica no-relativista deben coincidir con los resultados de la mecánica clásica cuando en ellos se practica adecuadamente el límite clásico. Así por ejemplo el límite clásico de la ecuación de Schrödinger para la función de onda dada por: Resulta idéntica a la ecuación de Hamilton-Jacobi de la mecánica clásica. Un cálculo directo lleva de hecho a que la ecuación de Schrödinger con la substitución anterior se puede escribir como:
Interpretando la fase de la onda Límite clásico de la mecánica relativistaSi en la especial, si consideramos que el espacio es plano y las velocidades son pequeñas (en comparación con la velocidad de la luz), encontramos que los objetos nuevamente parecen obedecer a la mecánica clásica. La teoría general de la relatividad requiere además de lo anterior que el espacio sea casi plano. Dicha condición requiere, además de que la pequeñez de velocidades, que los campos gravitatorios de las masas sean pequeños, condición que se cumple aceptablemente siempre que las distancias entre las partículas estén sean pequeñas en relación a su masa: (1) Límite clásico de la relatividad especialLa mayoría de ecuaciones de la teoría de la relatividad especial convergen a la expresión clásica sin más que hacer formalmente tender el parámetro que da la velocidad de la luz a infinito. En algunas otras expresiones se requiere restar primero una constante aditiva que no se refleja en las ecuaciones clásicas:
(2)
(3)
(4)
(5) Límite clásico de la relatividad generalCategoría: Mecánica cuántica |
|
| Este articulo se basa en el articulo Límite_clásico publicado en la enciclopedia libre de Wikipedia. El contenido está disponible bajo los términos de la Licencia de GNU Free Documentation License. Véase también en Wikipedia para obtener una lista de autores. |

Último visto

 .
.
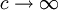 .
.


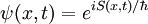
![\frac{\partial S}{\partial t}+\frac{1}{2m}\left[\left(\frac{\partial S}{\partial x}\right)^2 + \left(\frac{\partial S}{\partial y}\right)^2 + \left(\frac{\partial S}{\partial z}\right)^2 \right] + V(x) = \frac{i\hbar}{2m} \Delta S](images/math/5/a/a/5aa9eaa9dc70b6eac11f21868d9145e9.png)
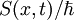 como la magnitud de acción dividida de la constante de Planck, y haciendo tender esta a cero se llega al límite clásico. Puede verse alternativamente que a medida que la masa del objeto es más y más grande se recupera igualmente el límite clásico. Lo cual explica porqué los cuerpos macroscópicos se comportan "clásicamente" aún cuando la constante de Planck no sea exactamente cero.
como la magnitud de acción dividida de la constante de Planck, y haciendo tender esta a cero se llega al límite clásico. Puede verse alternativamente que a medida que la masa del objeto es más y más grande se recupera igualmente el límite clásico. Lo cual explica porqué los cuerpos macroscópicos se comportan "clásicamente" aún cuando la constante de Planck no sea exactamente cero.
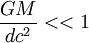 ,
,
![E_c = \lim_{c \to \infty} \frac{mc^2}{\sqrt{1-\frac{v^2}{c^2}}}-mc^2= \lim_{c \to \infty} mc^2\left [\frac{1}{2}\left(\frac{v^2}{c^2}\right)+ \frac{3}{8}\left(\frac{v^2}{c^2}\right)^2+\ldots \right] = \frac{1}{2}mv^2](images/math/f/0/3/f03707399951d52c6654c61df5e2ba62.png) ,
,
![\mathbf{p} = \lim_{c \to \infty} \frac{m\mathbf{v}}{\sqrt{1-\frac{v^2}{c^2}}}= \lim_{c \to \infty} m\mathbf{v}\left [1+\frac{1}{2}\left(\frac{v^2}{c^2}\right) \ldots \right] = m\mathbf{v}](images/math/2/3/1/231d78c99d2c2aec1a6da5c4dead042e.png) ,
,
![L +mc^2 = \lim_{c \to \infty} -mc^2{\sqrt{1-\frac{v^2}{c^2}}} +mc^2= \lim_{c \to \infty} +mc^2-mc^2\left [1-\frac{1}{2}\left(\frac{v^2}{c^2}\right) -\frac{1}{8}\left(\frac{v^2}{c^2}\right)^2 \ldots \right] = \frac{1}{2}mv^2](images/math/7/8/f/78f352cf6313ef3b02e3f1583913821e.png)
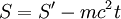
![\begin{matrix} \left(\frac{\part S}{\part x}\right)^2 + \left(\frac{\part S}{\part y}\right)^2 + \left(\frac{\part S}{\part z}\right)^2 - \frac{1}{c^2}\left(\frac{\part S}{\part t}\right)^2 = -m_0^2c^2 \mapsto \\ \mapsto \frac{1}{2m}\left[ \left(\frac{\part S'}{\part x}\right)^2 + \left(\frac{\part S'}{\part y}\right)^2 + \left(\frac{\part S'}{\part z}\right)^2 \right] - \frac{1}{2mc^2}\left(\frac{\part S'}{\part t}\right)^2 + \frac{\part S'}{\part t} = 0 \end{matrix}](images/math/9/6/a/96a323c6b98098019d3478cd782324d9.png)


