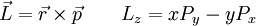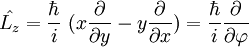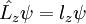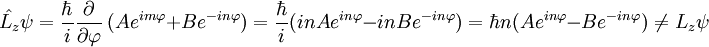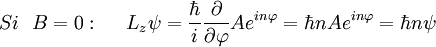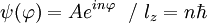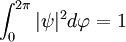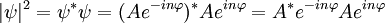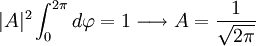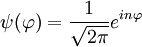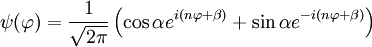|
La partícula en un anillo es ejemplo sencillo de sistema cuántico con propiedades interesantes. El modelo reproduce las características hipotéticas de una partícula libre que pudiera moverse de manera solamente a lo largo de un anillo (espacio topológico homeomorfo a S1) y de manera uniforme. Además en modelo aquí presentado ha encontrado aplicación en explicar la regla de Hückel sobre la estabilidad de los hidrocarburos aromáticos. Producto destacado
Descripción cuántica del sistemaSuponemos una partícula que se mueve libremente a lo largo de un anillo, las coordenadas de posición angular sobre el anillo y coordenadas cartesianas son: donde Buscamos la forma funciona de la energía clásica:
Operador hamiltonianoSi llamamos Donde E es el valor de la energía del estado, que por ser estacionario estará perfectamente bien definida. Ahora vamos a procurar transformar nuestra expresión de coordenadas cartesianas: Buscaremos las funciones propias del Hamiltoniano que son las que satisfacen la ecuación de Schrödinger independiente del tiempo: Soluciones de la ecuación de SchrödingerLos posibles estados estacionarios del sistema son las soluciones de la ecuación (1) anterior. Por otro lado, cualquier estado no estacionario será combinación de estados estacionarios de diferente energía. Como candidatos canónicos para representar los estados estacionarios debo escoger funciones propias del hamiltoniano, que por tanto deben ser solución de ecuación (1). En un sistema cuántico, puede pasar que existan diversos estados estacionarios con un mismo valor de la energía, esto es lo que va a suceder en el caso de la partícula en un anillo. Cuando eso sucde se dice que un estado de energía concreto presenta degeneración (un término poco explicativo que se introdujo por motivos históricos relacionados con el átomo de hidrógeno, pero que ha sido mantenido a pesar de ser poco explicativo). Puede verificarse fácilmente que las funciones trigonométricas seno y el coseno cumplen esos requisitos para ser mis funciones candidatas, aunque simplificar calculos, escogeremos exponenciales complejas que dependan de mi coordenada angular. Así buscamos candidatos a solución de la forma: Substituyendo esas funciones candidatas en la ecuación (1), se obtiene el valor necesario de k para que cualquiera de las dos sea solución:
Por lo tanto obtenemos nuestras funciones: Mi función (o vector) de estado, por tanto, debe de cumplir que sea una combinación lineal de ambas funciones: Número cuántico principalPara simplificar, definimos una constante matemática n que vamos a llamar simplemente número cuántico principal como: De nuevo, tendremos que imponer una condición para que mi función se comporte bien (well-behaviour function), en este caso, mi función tiene que ser continua en todos sus puntos y al dar una vuelta completa de mi partícula en el anillo, me tiene que dar el mismo valor, lo que nos lleva a imponer la siguiente condición de periodicidad: De hecho esa condición de periodicidad, no se da para cualquier valor del número cuántico n. Si estamos interesados sólo en los estados estacionarios que sí cumplen la condición de periodicidad y por tanto sí representan adecuadamente las restricciones físicas del problema debemos examinar que valores de n satisfacen la condición de periodicidad: Y de la última ecuación concluimos que sólo los valores enteros de n satisfacen la ecuación, los posibles valores del número cuántico principal son n = 0, 1, 2, 3... y n = -1, -2, -3... Es interesante notar que como consecuencia de exigir la condición periodicidad la energía del sistema está cuantizada:
DegeneraciónEl número cuántico n puede tomar, en este caso, el valor 0, porque no anula a mi función en el espacio. Y por otra parte tenemos que para dos números cuánticos que sean iguales y opuestos, se ve que obtenemos la misma energía (al estar n al cuadrado): a esto se le llama que los estados de energía definida son degenerados ya que existen varios estados de la misma energía. Sin embargo, esos estados de misma energía no son del todo idénticos como veremos, puesto que sobre ellos podemos medir otras magnitudes físicas diferentes de la energía y podemos ver que arrojan valores diferentes, lo cual significa que existe un procedimiento físico para distinguir entre estados "degenerados" de la misma energía. Esto se puede comprobar introduciendo el momento angular.
Momento angularA continuación veremos el momento angular de la partícula, es decir, vamos a ver si el operador Construimos el correspondiente operador cuántico: No es una función propia. Pero yo tengo infinitas funciones que determinan mi estado, como tal podré escoger un subconjunto propio de ellas en este caso: Y compruebo que efectivamente existe un subconjunto que es propio, en este caso sí es función propia de Lz: Con esta magnitud acabo de romper la degeneración de la energía, pudiendo distinguir dos estados que tienen distinto valor de momento angular. Normalización de los estados propios de momento angularPor último, para poder determinar el valor de A, y que nuestra función en el espacio valga 1, normalizamos a todo el espacio: Con la cual la función normaliada salvo fase es:
Estados estacionarios generales del sistemaPuede comprobarse que cualquier otro estado estacionario del sistema tiene la forma: Este estado tiene la propiedad interesante de que a pesar de que tiene una energía bien definida, su momento angular Lz no está bien definido, sino que una medida de esa magnitud con una probabilidad p1 da el valor +nh/2π y con una probabilidad p2 da el valor -nh/2π, cumpliéndose además: Aplicación a los hidrocarburos aromáticosEn química orgánica, los hidrocarburos aromáticos como el el benceno y otros, contienen estructuras en forma de anillo formado por cinco o seis átomos de carbono. Los experimentos muestran que estos compuestos químicos son extraordinariamente estables, debido a que de acuerdo con la discusión anterior los electrones se comportan como si estuvieran girando en ambas direcciones y están altamente deslocalizados. De acuerdo con el cálculo cuántico presentado anteriormente, rellenar todos los niveles de energía hasta el nivel n-ésimo requiere 2·(2n+1) electrones (donde el factor 2 inicial procede del hecho de que los electrones tienen dos posibles valores de espín). Esa es precisamente la Regla de Hückel que afirma que un exceso de 4n+2 electrones en un anillo de Kekulé produce un compuesto aromático excepcionalmente estable. Categoría: Mecánica cuántica |
|
| Este articulo se basa en el articulo Partícula_en_un_anillo publicado en la enciclopedia libre de Wikipedia. El contenido está disponible bajo los términos de la Licencia de GNU Free Documentation License. Véase también en Wikipedia para obtener una lista de autores. |




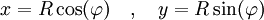
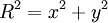 .
Los operadores de momento lineal vienen dados por:
.
Los operadores de momento lineal vienen dados por:
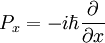
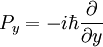
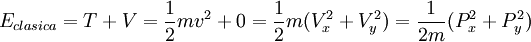
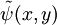 a la
a la 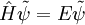
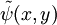 a coordenadas polares:
a coordenadas polares: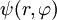 :
:
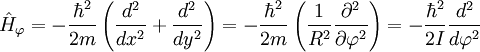
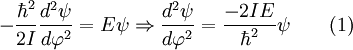

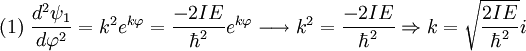
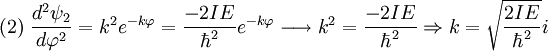
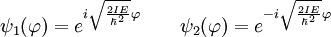
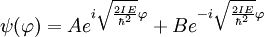
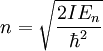
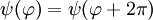
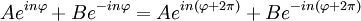
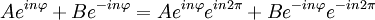
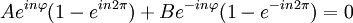
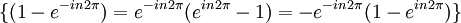
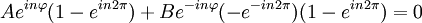
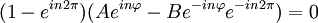
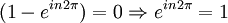
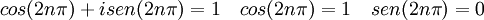
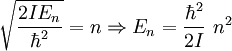
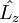 se comporta correctamente, partiendo de las expresiones clásicas:
se comporta correctamente, partiendo de las expresiones clásicas: