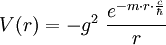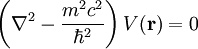Potencial de Yukawa

El potencial de Yukawa (también denominado potencial de Coulomb apantallado) es un potencial de la forma:

$V(r)= -g^2 \;\frac{e^{-m \cdot r \cdot \frac{c}{\hbar}}}{r}$

Conocimientos adicionales recomendados

Procedimientos normalizados de trabajo (PNT) para la comprobación de balanzas

Cómo realizar un pesaje correcto

8 pasos para limpiar una balanza y 5 soluciones para mantenerla limpia

Historia

Hideki Yukawa demostró en los 30 que ese potencial aparece por el intercambio de campos escalares masivos, como puede ser el campo del pión, cuya masa es $m π$ . Ya que el campo mediador es masivo, la fuerza correspondiente tiene un cierto rango debido a su decaimiento, siendo el rango invérsamente proporcional a la masa. Cuando la masa es nula el potencial de Yukawa se convierte en un potencial de Coulomb, que posee un rango infinito.

En la ecuación dada, el potencial es negativo, denotando que la fuerza resultante es atractiva. La constante g es un número real llamada constante de acoplamiento entre el campo de mesones y el campo fermiónico con los que interactúa. En física nuclear, los fermiones pueden ser tanto el protón como el neutrón.

Propiedades

El potencial de Yukawa de un conjunto estacionario de partículas satisface la ecuación de Helmholtz:

$\left(\nabla^2 - \frac{m^2c^2}{\hbar^2}\right)V(\mathbf{r}) = 0$

Categoría: Física nuclear

Este articulo se basa en el articulo Potencial_de_Yukawa publicado en la enciclopedia libre de Wikipedia. El contenido está disponible bajo los términos de la Licencia de GNU Free Documentation License. Véase también en Wikipedia para obtener una lista de autores.

Los portales especializados de LUMITOS