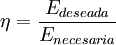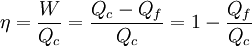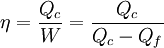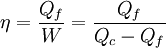Rendimiento térmico

El rendimiento térmico o eficiencia de una máquina térmica es una magnitud de proceso y adimensional, definida como el cociente de la energía que deseamos obtener de dicha máquina y la energía que se debe transferir para su funcionamiento. Se designa con la letra griega η:

Conocimientos adicionales recomendados

¿Cómo garantizar resultados de pesaje exactos cada día?

8 pasos para limpiar una balanza y 5 soluciones para mantenerla limpia

Cómo comprobar rápidamente el rendimiento de las pipetas

Dependiendo del tipo de máquina térmica considerada, la transferencia de estas energías se realizará en forma de calor, Q, o de trabajo, W.

Historia

En 1824, el físico francés Sadi Carnot derivó la eficiencia térmica para una máquina térmica ideal como una función de la temperatura de sus reservorios fríos y calientes:

donde

T_H es la temperatura del reservorio caliente;

T_C es la temperatura del reservorio frío.

La ecuación demuestra que se obtienen mayores niveles de eficiencia con un mayor gradiente de temperatura entre los fluidos calientes y fríos. En la práctica, cuanto mas caliente el fluido, mayor será la eficiencia del motor.

Cálculo del rendimiento para las distintas máquinas térmicas

• El motor térmico recibe un calor, Q_c, de un foco o fuente caliente, efectúa un trabajo, W, y debe ceder calor, Q_f, a un foco frío. Para que la energía se conserve debe cumplirse que Q_c = W + Q_f. El rendimiento es por lo tanto:

donde se cumple que 0<η<1.

• La bomba térmica o de calor es capaz de transferir una energía calorífica, Q_c, a un foco caliente desde una fuente fría de la que absorbe un calor, Q_f, si se realiza un determinado trabajo, W, sobre la máquina. Este proceso es justo el opuesto al realizado por el motor térmico, es por ello que también debe cumplirse la relación Q_c = W + Q_f. El rendimiento es:

y se tiene que η>1.

• El refrigerador funciona exáctamente igual que la bomba térmica pero como el interés de ésta máquina es enfriar, la transferencia de energía deseada es Q_f y el rendimiento queda como:

donde ahora η>0.