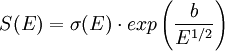|
En física nuclear, la sección eficaz (cross section en inglés) se define como la probabilidad de interacción entre dos partículas. Es una magnitud de superficie normalmente representada con la letra sigma y se suele medir en barns: 1b = 10 − 24cm2 Conocimientos adicionales recomendadosEstadísticamente los núcleos de los átomos de una placa se pueden considerar como diminutos circulitos de radio r distribuidos a lo largo de un plano de superficie A. En el diagrama siguiente se representan un grupo de partículas a que inciden a velocidad V sobre un grupo de partículas X que actúan como blanco de las primeras. Así la probabilidad de impactar contra una de esas partículas distribuidas en la lamina será de (nπr2)/A. Donde n representa el número de partículas X distribuidas en la superficie A. El diámetro nuclear típico es de unos 10−12 cm por lo que las secciones eficaces entre núcleos son del orden de 10−24 cm2 valor al que se le dio una unidad propia, el barn. Dependiendo de qué reacciones se trate las secciones eficaces pueden variar enormemente yendo desde los 1.000 barns hasta los 0.001 barn. Las partículas X al recibir el impacto de las a dan, como resultado, un núcleo excitado que se desintegra tras la fusión dando lugar a una serie de posibilidades distintas o canales de salida, cada uno con su probabilidad de ocurrencia. 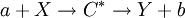 La sección eficaz de las reacciones entre dichas partículas se calcula como sigue:
Donde Γa representa la anchura del nivel de energía de la partícula a y Γ la anchura total. λ es la longitud de onda de De Broglie y f(E) es el factor de forma. Su valor dependerá de si hay resonancia nuclear o no. Si no la hay su valor será constante. Así pues:
En caso de que la energía de fusión entre las partículas a y X coincida con la de alguno de los niveles de energía se da un fenómeno llamado resonancia nuclear entonces el factor de forma se torna dependiente de la energía y vale: Donde Eres es la energía de resonancia. Como se puede ver fácilmente a poco que E se aleje de Eres el término dejará de contribuir por lo que se lo puede considerar como un pico de Dirac. Dependencia de la energía de σ(E)La sección eficaz es un parámetro altamente dependiente de la energía por ello resulta complicado especular sus valores a bajas energías, más allá de donde obtenemos datos experimentales. A altas energías no nos es difícil obtener datos ya que la probabilidad de ocurrencia de las reacciones es alta pero a bajas energías la probabilidad es tan baja que con las muestras de partículas con las que se trabaja nunca ocurre nada. Según la fórmula que se ha dado de la sección eficaz la dependencia de la energía sería como sigue:
Para resolver este problema se ha creado, a partir de la sección eficaz, el factor astrofísico (S(E)) mucho menos dependiente de E lo que lo hace más fácilmente extrapolable. Se usa, sobre todo, en astrofísica porque cambia poco a lo largo de la vida de una estrella. Como se ve, lo que se ha hecho es quitarle la dependencia respecto al factor de penetración. Sección eficaz macroscópicaAl producto Σ = Nσ(E) se le denomina sección eficaz macroscópica, siendo N la densidad de partículas blanco que pueden interaccionar. Las unidades resultantes para la sección eficaz macroscópica son de longitud inversa. Véase también:
Categoría: Física nuclear y de partículas |
| Este articulo se basa en el articulo Sección_eficaz publicado en la enciclopedia libre de Wikipedia. El contenido está disponible bajo los términos de la Licencia de GNU Free Documentation License. Véase también en Wikipedia para obtener una lista de autores. |


Enciclopedia




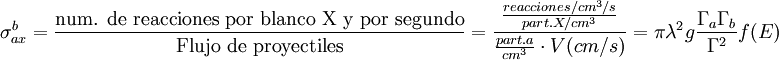
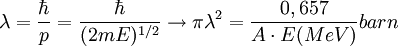
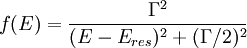
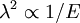 Este es el
Este es el  Esto es el factor de penetración de la barrera culombiana (Más información en: Pico de Gamow).
Esto es el factor de penetración de la barrera culombiana (Más información en: Pico de Gamow).
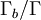 Depende poco.
Depende poco.
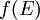 Solo depende en un estrecho margen en las cercanías de la resonancia nuclear, normalmente es constante.
Solo depende en un estrecho margen en las cercanías de la resonancia nuclear, normalmente es constante.