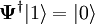Segunda cuantización

La segunda cuantificación es un formalismo matemático de cuantización empleado para estudiar tanto sistemas de muchas partículas idénticas con interacciones arbitrarias como la teoría cuántica de campos. El teorema espín-estadística dentro lleva a establecer relaciones de conmutación que clasifican a las partícuas en bosones y fermiones.

Producto destacado

Software fácil de usar para el diseño de experimentos (DoE) sin esfuerzo

La mezcladora centrífuga planetaria Thinky ARE-312

Historia

El formalismo de segunda cuantización fue iniciado por Paul M. Dirac para los bosones y fue extendido a los fermiones por Eugene Wigner y Pascual Jordan. La importancia y utilidad de la segunda cuantificación estriba en que:

• Permite estudiar los campos físicos desde el punto de vista cuántico.
• Permite tomar en cuenta automáticamente en los cálculos los aspectos combinatorios que derivan de la estadística apropiada al tipo de partículas del sistema.
• Además, facilita extender la mecánica cuántica no relativa a sistemas en los cuales el número de partículas no es una constante del movimiento.

En el dominio relativista, donde las antipartículas emergen de un modo natural, y los procesos de creación de pares partícula-antipartícula están presentes se requiere una teoría donde el número de partículas no necesariamente permanezca constante y por tanto requiere un tratamiento como el de la segunda cuantización.

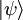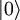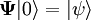
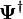Si es la función de onda para una partícula, con la segunda cuantización pasaría a ser un operador no-hermítico Ψ que actúa sobre un estado del espacio-tiempo, como por ejemplo el que representa el vacío . La actuación del operador sobre dicho estado representa el estado del espacio-tiempo una vez se ha creado una partícula con esa función de onda habiendo dejado de ser el estado vacío:

De estas forma se interpreta que Ψ "crea" una partícula en el estado mencionado. Su operador adjunto "destruiría" dicha partícula (o equivalentemente crearía una antipartícula). Sí 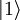donta un estado con una partícula del tipo correcto entonces: