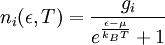Estadística de Fermi-Dirac

La estadística de Fermi-Dirac es la forma de contar estados de ocupación de forma estadística en un sistema de fermiones. Forma parte de la Mecánica Estadística. Y tiene aplicaciones sobre todo en la Física del estado sólido.

La energía de un sistema mecanocuántico está discretizada. Esto quiere decir que las partículas no pueden tener cualquier energía, sino que ha de ser elegida de entre un conjunto de valores discreto. Para muchas aplicaciones de la física es importante saber cuántas partículas están a un nivel dado de energía. La distribución de Fermi-Dirac nos dice cuánto vale esta cantidad en función de la temperatura y el potencial químico.

Conocimientos adicionales recomendados

Cómo comprobar rápidamente el rendimiento de las pipetas

8 pasos para limpiar una balanza y 5 soluciones para mantenerla limpia

Cómo realizar un pesaje correcto

Formulación matemática

La distribución de Fermi-Dirac viene dada por

Donde:

n_i el número promedio de partículas en el estado de energíaε_i.

g_i es la degeneración el estado i-ésimo

ε_i es la energía en el estado i-ésimo

μ es el potencial químico

T es la temperatura

k_B la constante de Boltzmann

Interpretación Física

Para bajas temperaturas, la distribución de fermi es una función escalón que vale 1 si ε < μ y 0 si ε > μ. Esto quiere decir que las partículas van colocando desde el nivel más bajo de energía hacia arriba debido al Principio de exclusión de Pauli hasta que se hayan puesto todas las partículas. La energía del último nivel ocupado se denomina energía de Fermi y la temperatura a la que corresponde esta energía mediante ε_f = k_BT_f temperatura de Fermi.

Se da la circunstancia de que la temperatura de Fermi de la mayoría de metales reales es enorme (del orden de 10000 Kelvin), por tanto la aproximación de decir que la distribución de Fermi-Dirac sigue siendo un escalón hasta temperatura ambiente es válida con bastante precisión.

La distribución de Fermi-Dirac tiene importancia capital en el estudio de gases de fermiones y en particular en el estudio de los electrones libres en un metal.

Aplicaciones

Véase también

• Fermión
• Estadística de Bose-Einstein
• Principio de exclusión de Pauli

Enlaces externos

Una explicación completa y asequible de la función de Fermi