Potencial de Lennard-Jones
Un par de átomos o moléculas neutros estan sujetos a dos fuerzas distintas en el limite de una gran separación y de una pequeña separación: una fuerza atractiva actúa a grandes distancias (fuerza de Van Der Waals, o fuerza de dispersión) y una fuerza repulsiva actuando a pequeñas distancias (el resultado de la sobreposición de los orbitales electrónicos, conocido como la repulsión de Pauli, del Principio de exclusión de Pauli). El Potencial de Lennard-Jones (También conocido como el potencial L-J, el potencial 6-12 o, con menor frecuencia, como el potencial 12-6) es un modelo matemático sencillo para representar este comportamiento. Fue propuesto en 1924 por John Lennard-Jones.[1]
EL potencial L-J es de la forma
![V(r) = 4\epsilon \left[ \left(\frac{\sigma}{r}\right)^{12} - \left(\frac{\sigma}{r}\right)^{6} \right]](images/math/e/a/c/eac9407d601624e0d5123ae78ccc1127.png)
donde 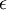 es la profundidad del potencial, es la profundidad del potencial, 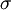 es la distancia (finita) en la que el potencial entre partículas es cero y r es la distancia entre partículas. es la distancia (finita) en la que el potencial entre partículas es cero y r es la distancia entre partículas.
Estos parámetros pueden ser ajustados para rerpoducir datos experimentales o pueden ser deducidos de resultados muy precisos de cálculos de quimica cuantica. El término
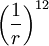 describe la repulsión y el termino describe la repulsión y el termino
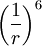 describe la atracción.
La función que describe la fuerza a la que estan sujetas las partículas es el negativo del gradiente del potencial arriba descrito describe la atracción.
La función que describe la fuerza a la que estan sujetas las partículas es el negativo del gradiente del potencial arriba descrito
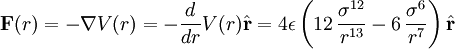
El potencial de Lennard-Jones es una aproximación. La forma del término que describe la repulsión no tiene ninguna justificación teórica; la fuerza repulsiva debe depender exponencialmente de la distancia, pero el termino de la formula de L-J es mas conveniente debido a la facilidad y eficiencia de calcular r12 como el cuadrado de r6. Su origen físico esta relacionado al principio de exclusión de Pauli: cuando dos nubes electrónicas circulando los átomos se empiezan a sobreponer, la energía del sistema aumenta abruptamente. El exponente 12 fue elegido exclusivamente por su facilidad de calculo.
Formas alternativas
La función del potencial de Lennard-Jones comúnmente se escribe de la siguiente forma:
![V(r) = \epsilon \left[ \left(\frac{r_{min}}{r}\right)^{12} - 2\left(\frac{r_{min}}{r}\right)^{6} \right]](images/math/d/9/2/d9283be3ed70576130d56caa6710c081.png)
donde
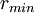 = = 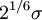 es la distancia en la que el potencial se encuentra en un mínimo. es la distancia en la que el potencial se encuentra en un mínimo.
La formulación más sencilla, usada comúnmente por software de simulación, es:
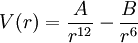
donde
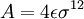
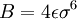
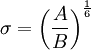
y
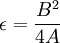 . .
Simulación de Dinámica Molecular: Potencial truncado
En general, para ahorrar tiempo computacional, el potencial de Lennard-Jones es truncado en la distancia límite de
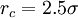 donde
donde
|
![\displaystyle V ( r_c ) = V ( 2.5 \sigma ) = 4 \epsilon \left[ \left( \frac {\sigma} {2.5 \sigma} \right)^{12} - \left( \frac {\sigma} {2.5 \sigma} \right)^6 \right] = -0.0163 \epsilon = - \frac {1} {61.3} \epsilon](images/math/b/e/f/bef09563e5795f7567db0ac31a3378f7.png)
| (1)
|
i.e., en
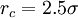 , el potencial LJ , el potencial LJ
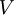 es aproximadamente 1/60 de su valor mínimo es aproximadamente 1/60 de su valor mínimo
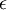 (profundidad del potencial).
Después de
(profundidad del potencial).
Después de
 , se le asigna el valor 0 al potencial computacional. , se le asigna el valor 0 al potencial computacional.
Por otro lado, para evitar una discontinuidad en
 ,
como se muestra en la ecuación 1, el potencial de LJ es desplazado ligeramente hacia arriba, de tal forma que el potencial computacional sea 0 exactamente en la distancia límite ,
como se muestra en la ecuación 1, el potencial de LJ es desplazado ligeramente hacia arriba, de tal forma que el potencial computacional sea 0 exactamente en la distancia límite
 . .
Referencias
- ↑ Lennard-Jones, J. E. Cohesion. Proceedings of the Physical Society 1931, 43, 461-482.
|




![V(r) = 4\epsilon \left[ \left(\frac{\sigma}{r}\right)^{12} - \left(\frac{\sigma}{r}\right)^{6} \right]](images/math/e/a/c/eac9407d601624e0d5123ae78ccc1127.png)
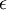 es la profundidad del potencial,
es la profundidad del potencial, 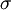 es la distancia (finita) en la que el potencial entre partículas es cero y r es la distancia entre partículas.
es la distancia (finita) en la que el potencial entre partículas es cero y r es la distancia entre partículas.
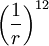 describe la repulsión y el termino
describe la repulsión y el termino
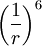 describe la atracción.
La función que describe la fuerza a la que estan sujetas las partículas es el negativo del gradiente del potencial arriba descrito
describe la atracción.
La función que describe la fuerza a la que estan sujetas las partículas es el negativo del gradiente del potencial arriba descrito
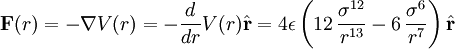
![V(r) = \epsilon \left[ \left(\frac{r_{min}}{r}\right)^{12} - 2\left(\frac{r_{min}}{r}\right)^{6} \right]](images/math/d/9/2/d9283be3ed70576130d56caa6710c081.png)
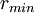 =
= 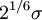 es la distancia en la que el potencial se encuentra en un mínimo.
es la distancia en la que el potencial se encuentra en un mínimo.
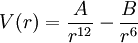
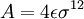
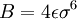
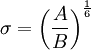
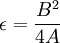 .
.
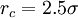 donde
donde
![\displaystyle V ( r_c ) = V ( 2.5 \sigma ) = 4 \epsilon \left[ \left( \frac {\sigma} {2.5 \sigma} \right)^{12} - \left( \frac {\sigma} {2.5 \sigma} \right)^6 \right] = -0.0163 \epsilon = - \frac {1} {61.3} \epsilon](images/math/b/e/f/bef09563e5795f7567db0ac31a3378f7.png)
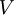 es aproximadamente 1/60 de su valor mínimo
es aproximadamente 1/60 de su valor mínimo
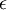 (profundidad del potencial).
Después de
(profundidad del potencial).
Después de
 , se le asigna el valor 0 al potencial computacional.
, se le asigna el valor 0 al potencial computacional.


