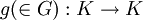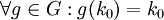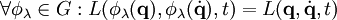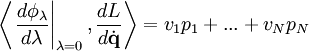Simetría

La simetría es un rasgo característico de formas geométricas, sistema, ecuaciones, y otros objetos materiales o entidades abstractas.

En condiciones formales, decimos que un objeto es simétrico en lo que concierne a una operación matemática dada, si, cuando aplicado al objeto, esta operación no cambia el objeto o su aspecto. Dos objetos son simétricos uno al otro en lo que concierne a un grupo dado de operaciones si uno es obtenido de otro por algunas operaciones (y viceversa). En la geometría 2D las clases principales de simetría de interés son las que conciernen a las isometrías de un espacio euclídeo: traslaciones, rotaciones, reflexiones y reflexiones que se deslizan.

La simetría también puede ser encontrado en organismos vivos.

Conocimientos adicionales recomendados

8 pasos para limpiar una balanza y 5 soluciones para mantenerla limpia

Cómo realizar un pesaje correcto

¿Cómo garantizar resultados de pesaje exactos cada día?

Tabla de contenidos

1 Simetría en geometría
2 Simetría en física
3 Simetría en alimentación de AC
4 Simetría en química
5 Simetría en biología
- 5.1 Simetría radial
- 5.2 Simetría bilateral
6 Referencias

Simetría en geometría

Cuando hablamos de objetos físicos o elementos geométricos el concepto de simetría está asociado a transformaciones geométricas tales como las rotaciones, las reflexiones o las traslaciones. Así se dice que un objeto presenta:

Simetría esférica si existe simetría bajo cualquier rotación posible, matemáticamente equivale a que el grupo de simetría de un objeto físico o entidad matemática sea SO(3).
Simetría cilíndrica o axial, si existe un eje tal que los giros alrededor de él no conducen a cambios de posición en el espacio, matemáticamente está asociado a un grupo de isometría SO(2).
Simetría reflectiva,se define por la existencia de un único plano, matemáticamente está asociado al grupo SO(1) o su representación equivalente $\mathbb{Z}_2$ .

Si tratamos además de regiones geométricas infinitas, no acotadas, además puede existir simetría traslacional. Todas estas simetrías posibles son además isometrías.

Simetría en física

En física el concepto de simetría puede formularse en una forma no geométrica. Si K es un conjunto de objetos matemáticos del mismo tipo (funciones, formas geométricas, ecuaciones, ...) y G es un grupo de transformaciones que actúa sobre K de tal manera que:

$g (\in G): K \to K$

Se dice que un elemento de k₀ presenta simetría si:^[1]

$\forall g\in G: g(k_0) = k_0$

Así por ejemplo varias leyes de conservación de la física son consecuencia de la existencia de simetrías abstractas del lagrangiano, tal como muestra el teorema de Noether. En ese caso K representaría el conjunto de lagrangianos admisibles, k₀ el lagrangiano del sistema bajo estudio y G puede representar traslaciones espaciales (conservación del conservación del momento lineal), traslaciones temporales (conservación de la energía), rotaciones (conservación del momento angular) u otro tipo de simetrías abstractas (conservación de la carga eléctrica, el número leptónico, la paridad, etc.).

Ejemplo 1. Como primer ejemplo consideremos un electrón moviéndose entre dos placas infinitas cargadas uniformemente (dicho sistema se aproxima cierto tipo de condesadores), dado que cualquier tralación paralela a los planos constituye una simetría del sistema físico, entonces tanto la fuerza paralela a dichos planos es nula y por tanto la velocidad paralela a los planos es constante.

Ejemplo 2. Consideremos un satélite orbitando alredodor de un astro (planeta o estrella) con simetría esférica perfecta, consideremos además que la velocidad del satelite sea perpendicular a la línea entre el centro del satélite y el astro. En ese caso, el lagrangiano es totalmente invariante respecte a rotaciones según un eje que pase por el centro de la fuente del campo gravitatorio. En este caso debido a la simetría de rotación tanto del lagrangiano como de las condiciones iniciales del movimiento, la velocidad perpendicular al planeta es constante y la trayectoria es un círculo invariante bajo una rotación perpendicular al plano de la órbita.

Estos dos ejemplos anteriores son casos del teorema de Noether, un resultado general que establece que si existe un grupo uniparamétrico de simetría G para el lagrangiano tal que:

$\forall \phi_\lambda\in G: L(\phi_\lambda(\mathbf{q}),\phi_\lambda(\dot\mathbf{q}),t) = L(\mathbf{q},\dot\mathbf{q},t)$

Entonces la cantidad escalar:

$\left \langle \left . \frac{d\phi_\lambda}{d\lambda}\right \vert_{\lambda=0}, \frac{dL}{d\dot\mathbf{q}}\right\rangle = v_1p_1 + ... + v_Np_N$

Siendo v el campo vectorial que general el grupo uniparamétrico de transformaciones de simetría, y p_i los momentos conjungados de las coordenadas generalizadas de posición.

Simetría en alimentación de AC

En el contexto de la electrónica de radiofrecuencia, se habla de una alimentación simétrica de AC cuando ninguno de los conductores está a la masa. Cuando uno de los conductores está a la masa y el otro experimenta las variaciones de tensión, se dice que la alimentación es asimétrica.

Existen importantes aplicaciones tecnológicas basadas en la alimentación simétrica, ya que la alimentación simétrica tiene la gran ventaja de que la pérdida de potencia en la línea de transmisión es un orden de magnitud menor que la alimentación asimétrica por cable coaxial.

En efecto, el campo alterno generado por el conductor ascendente es cancelado por el campo generado por su homólogo descendente.
Además, la alimentación simétrica en delta permite la simplificación de la construcción.

La alimentación simétrica es por lo tanto la alimentación preferida en la operación QRP y en el modo EME, modos donde cada dB de ganancia cuenta.

Simetría en química

Artículo principal: Simetría molecular

En química la simetría geométrica de las moléculas es muy importante, ya que permite clasificar las moléculas. Además propiedades como su momento dipolar y las transiciones espectroscópicas permitidas (basadas en reglas de selección como la regla de Laporte) pueden predecirse o ser explicadas a partir de la simetría de la molécula. Las simetrías que aparecen en química están asociadas a grupos finitos de isometrías, en concreto son grupos puntuales de transformaciones de isometría.

Simetría en biología

Simetría en biología es la equilibrada distribución en el cuerpo de los organismos de aquellas partes que aparecen duplicadas. Los planes corporales de la mayoría de organismos pluricelulares exhiben alguna forma de simetría, bien sea simetría radial o simetría bilateral. Una pequeña minoría no presenta ningún tipo de simetría (son asimétricos).

Simetría radial

Artículo principal: Simetría radial

La simetría radial es la simetría definida por un eje heteropolar (distinto en sus dos extremos). El extremo que contiene la boca se llama lado oral, y su opuesto lado aboral o abactinal. Sobre este eje, se establecen planos principales de simetría; dos perpendiculares que definen las posiciones per-radiales. Las estructuras en otros planos (bisectrices de los per-radiales) quedan en posiciones inter-radiales. La zona entre los per-radiales y los inter-radiales es la zona ad-radial.

Simetría bilateral

Artículo principal: Simetría bilateral

La mayoría de especies animales tiene simetría bilateral y pertenece por tanto al grupo Bilateria, aunque hay especies como los erizos y las estrellas de mar que presentan simetría radial secundaria (las fases de desarrollo tempranas y las larvas poseen simetría bilateral que posteriormente se pierde en el adulto). La simetría bilateral permite la definición de un eje corporal en la dirección del movimiento, lo que favorece la formación de un sistema nervioso centralizado y la cefalización.

Referencias

↑ Wald, 1984, p. 441-444.

Robert M. Wald: General relativity, Chicago University Press, 1984, ISBN 0-226-87032-4.

Categoría: Anatomía

Este articulo se basa en el articulo Simetría publicado en la enciclopedia libre de Wikipedia. El contenido está disponible bajo los términos de la Licencia de GNU Free Documentation License. Véase también en Wikipedia para obtener una lista de autores.