|
Producto destacado
Momento angular en mecánica clásicaEn mecánica newtoniana,la cantidad de movimiento angular de una masa puntual, es igual al producto vectorial del vector de posición En ausencia de momentos de fuerzas externos, el momento angular de un conjunto de partículas, de objetos o de cuerpos rígidos se conserva. Esto es válido tanto para partículas subatómicas como para galaxias. Momento angular de una masa puntual
En el dibujo de derecha vemos una masa El vector El módulo del momento angular es: Es decir, el módulo es igual al momento lineal multiplicado por su brazo ( Dependencia temporalDerivemos el momento angular con respecto al tiempo: El primero de los paréntesis es cero ya que la derivada de donde La derivada temporal del momento angular es igual al torque aplicado a la masa puntual. Momento angular de un conjunto de partículas puntualesEl momento angular de un conjunto de partículas es la suma de los momentos angulares de cada una: La variación temporal es: El término de derecha es la suma de todos los torques producidos por todas las fuerzas que actúan sobre las partículas. Una parte de esas fuerzas puede ser de origen externo al conjunto de partículas. Otra parte puede ser fuerzas entre partículas. Pero cada fuerza entre partículas tiene su reacción que es igual pero de dirección opuesta y colineal. Eso quiere decir que los torques producidos por cada una de las fuerzas de un par acción-reacción son iguales y de signo contrario y que su suma se anula. Es decir, la suma de todos los torques de origen interno es cero y no puede hacer cambiar el valor del momento angular del conjunto. Solo quedan los torques externos: El momento angular de un conjunto de partículas se conserva en ausencia de torques externos. Esta afirmación es válida para cualquier conjunto de partículas: desde núcleos atómicos hasta grupos de galaxias. Momento angular de un sólido rígidoTenemos que en un sistema inercial la ecuación de movimiento es: Donde:
Ahora bien, normalmente para un sólido rígido el tensor de inercia
Donde Que resulta ser una ecuación no lineal en la velocidad angular. Conservación del momento angular clásicoCuando la suma de los torques externos es cero Eso quiere decir que Consideremos un objeto que puede cambiar de forma. En una de esas formas, su Momento de inercia es En algunos casos el momento de inercia se puede considerar un escalar. Entonces la dirección del vector velocidad angular no cambiará. Solo cambiará la velocidad de rotación. Hay muchos fenómenos en los cuales la conservación del momento angular tiene mucha importancia. Por ejemplo:
EjemploEn el dibujo de derecha tenemos una masa que gira, tenida por un hilo de masa despreciable que pasa por un tubito fino. Suponemos el conjunto sin frotamientos y no tenemos cuenta de la gravedad. La fuerza que el hilo ejerce sobre la masa es radial y no puede ejercer un torque sobre la masa. Si tiramos del hilo, el radio de giro disminuirá. Como, en ausencia de torques externos, el momento angular se conserva, la velocidad de rotación de la masa debe aumentar.
En el dibujo siguiente aparece la masa que gira con un radio o sea: Y, si multiplicamos por la masa Vemos como el momento angular se ha conservado: Para reducir el radio de giro hay que comunicar una velocidad radial, la cual aumenta la velocidad total de la masa. También se puede hacer el experimento en el otro sentido. Si se suelta el hilo, la masa sigue la tangente de la trayectoria y su momento angular no cambia. A un cierto momento frenamos el hilo para que el radio sea constante de nuevo. El hecho de frenar el hilo, comunica una velocidad radial (hacia el centro) a la masa. Esta vez esta velocidad radial disminuye la velocidad total y solo queda la componente de la velocidad tangencial al hilo en la posición en la cual se lo frenó. No es necesario de hacer la experiencia dando un tirón. Se la puede hacer de manera continua, ya que la fuerza que se hace recobrando y soltando hilo puede descomponerse en una sucesión de pequeños impulsos. Momento angular en mecánica relativistaEn mecánica newtoniana el momento angular es un pseudovector o vector axial, por lo que en mecánica relativista debe ser tratado como el dual de Hodge de las componentes espaciales de un tensor antisimétrico. Una representación del momento angular en la teoría especial de la relatividad es por tanto como cuadritensor antisimétrico:
Puede verse que las 3 componentes espaciales forman el momento angular de la mecánica newtoniana Momento angular en mecánica cuánticaEn mecánica cuántica, se transforma en un operador, análogamente al momento lineal: Usando coordenadas cartesianas las tres componentes del momento angular se expresan en el espacio de Hilbert usual para las funciones de onda, En cambio en coordenadas angulares esféricas el cuadrado del momento angular y la componente Z se expresan como: Las vectores propios o estados propios del momento angular cuántico dependen de dos números cuánticos enteros l y m, se designan como Estos vectores propios expresados en términos de las coordenadas angulares esféricas son los llamados armónicos esféricos Yl,m(θ,φ), que se construyen a partir de los polinomios de Legendre: Tienen especial importancia por ser la componente angular de los orbitales atómicos. Finalmente las relaciones de conmutación canónicas para los operadores momento angular son: donde εijk es el símbolo de Levi-Civita. Conservación del momento angular cuánticoEs importante notar que si el hamiltoniano no depende de las variables angulares, como sucede por ejemplo en problemas con potencial de simetría esférica entonces todas las componentes del momento angular conmutan con el hamiltoniano: y, como consecuencia, el cuadrado del momento angular también conmuta con el Hamiltoniano:
Y tenemos que el momento angular se conserva, eso significa que a lo largo de la evolución en el tiempo del sistema cuántico la distribución de probabilidad de los valores del momento angular no variará. Nótese sin embargo que como las componentes del momento angular no conmutan entre si no se pueden definir simultáneamente. Sin embargo, si se pueden definir simultáneamente el cuadrado del momento angular y una de sus componentes (habitualmente se elije la componente Z). En particular si tenemos estados cuánticos de momento bien definido estos seguirán siendo estados cuánticos de momento bien definido con los mismos valores de los números cuánticos l y m.
Véase tambiénCategoría: Mecánica cuántica |
|
| Este articulo se basa en el articulo Momento_angular publicado en la enciclopedia libre de Wikipedia. El contenido está disponible bajo los términos de la Licencia de GNU Free Documentation License. Véase también en Wikipedia para obtener una lista de autores. |





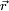 (brazo), del objeto en relación a la recta considerada como eje de rotación, por la cantidad de movimiento
(brazo), del objeto en relación a la recta considerada como eje de rotación, por la cantidad de movimiento 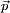 (también llamado momento lineal o momento). Frecuentemente se lo designa con el símbolo
(también llamado momento lineal o momento). Frecuentemente se lo designa con el símbolo 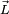 :
:
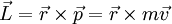
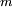 que se desplaza con una velocidad instantánea
que se desplaza con una velocidad instantánea 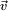 . El momento angular de esta partícula, con respecto a la recta perpendicular al plano que contiene
. El momento angular de esta partícula, con respecto a la recta perpendicular al plano que contiene 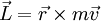
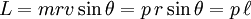
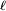 en el dibujo), el cual es la distancia entre el eje de rotación y la recta que contiene la velocidad de la partícula.
Por esta razón, algunos designan el momento angular como el "momento del momento".
en el dibujo), el cual es la distancia entre el eje de rotación y la recta que contiene la velocidad de la partícula.
Por esta razón, algunos designan el momento angular como el "momento del momento".
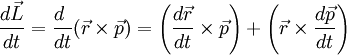
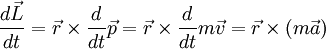
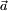 es la aceleración. Pero
es la aceleración. Pero 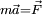 , la fuerza aplicada a la masa. Y el producto vectorial de
, la fuerza aplicada a la masa. Y el producto vectorial de 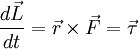
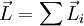
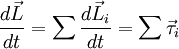
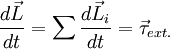
![\frac{d\vec{L}}{dt} = \frac{d}{dt}\left[\mathbf{I}(t) \vec{\omega}(t)\right]](images/math/c/b/d/cbdea8170e173efaac9f717c8fcb5330.png)
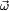 es la velocidad angular del sólido.
es la velocidad angular del sólido.
 es el tensor de inercia del cuerpo.
es el tensor de inercia del cuerpo.
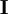 , depende del tiempo y por tanto en el sistema inercial generalmente no existe un análogo de la segunda ley de Newton, y a menos que el cuerpo gire alrededor de uno de los ejes principales de inercia sucede que:
, depende del tiempo y por tanto en el sistema inercial generalmente no existe un análogo de la segunda ley de Newton, y a menos que el cuerpo gire alrededor de uno de los ejes principales de inercia sucede que:
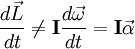
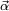 es la aceleración angular del cuerpo. Por eso resulta más útil plantear las ecuaciones de movimiento en un sistema no inercial formado por los ejes principales de inercia del sólido, así se logra que
es la aceleración angular del cuerpo. Por eso resulta más útil plantear las ecuaciones de movimiento en un sistema no inercial formado por los ejes principales de inercia del sólido, así se logra que 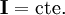 , aunque entonces es necesario contar con las fuerzas de inercia:
, aunque entonces es necesario contar con las fuerzas de inercia:
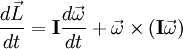
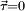 , hemos visto que:
, hemos visto que:
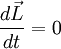
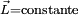 . Y como
. Y como 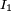 y su velocidad angular
y su velocidad angular 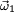 . Si el objeto cambia de forma (sin intervención de un torque externo) y que la nueva distribución de masas hace que su nuevo Momento de inercia sea
. Si el objeto cambia de forma (sin intervención de un torque externo) y que la nueva distribución de masas hace que su nuevo Momento de inercia sea 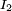 , su velocidad angular cambiará de manera tal que:
, su velocidad angular cambiará de manera tal que:
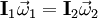
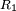 en el momento en el cual se da un tirón del hilo. El término correcto del "tirón" física es un impulso, es decir una fuerza aplicada durante un momento. Ese impulso comunica una velocidad radial
en el momento en el cual se da un tirón del hilo. El término correcto del "tirón" física es un impulso, es decir una fuerza aplicada durante un momento. Ese impulso comunica una velocidad radial 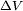 a la masa. La nueva velocidad será la suma vectorial de la velocidad precedente
a la masa. La nueva velocidad será la suma vectorial de la velocidad precedente 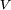 con
con 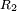 , cobramos el hilo suelto y la masa continuará a girar con el nuevo radio
, cobramos el hilo suelto y la masa continuará a girar con el nuevo radio 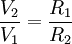
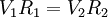
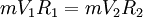
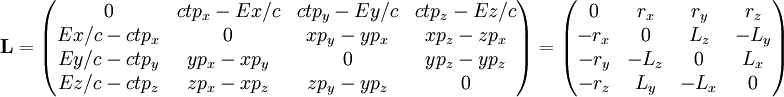
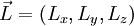 y el resto de componentes
y el resto de componentes 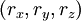 describen el momiviento del centro de masas relativista.
describen el momiviento del centro de masas relativista.
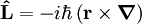
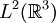 , como:
, como:
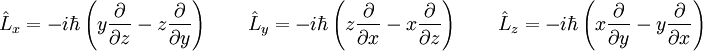
![\ \hat{L}^2 = -\hbar^2 \left[\frac{1}{\sin\theta}\frac{\partial}{\partial \theta}\left( \sin\theta \frac{\partial}{\partial \theta}\right) + \frac{1}{\sin^2\theta}\frac{\partial^2}{\partial \varphi^2} \right] \qquad \hat{L}_z = -i\hbar\left(\frac{\partial}{\partial \varphi}\right)](images/math/d/a/2/da27208af2090e099730117691b19b82.png)
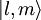 y satisfacen las relaciones:
y satisfacen las relaciones:
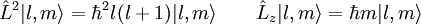
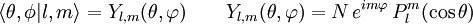
![[\hat{L}_i, \hat{L}_j ] = i \hbar \epsilon_{ijk} \hat{L}_k, \qquad \left[\hat{L}_i, \hat{L}^2 \right] = 0](images/math/d/a/a/daa3218f72149933033e8354260d9b6a.png)
![\left[\hat{L}_i, H \right] = 0](images/math/e/4/6/e46308ebc147de77a2aefd823a14e163.png)
![\left[\hat{L}^2, H \right] = 0](images/math/3/9/3/39301aa4d9e73eb0cea2a7f722a0e642.png) .
.


