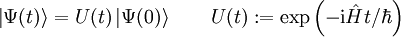|
El Hamiltoniano H tiene dos significados distintos, aunque relacionados. En mecánica clásica, es una función que describe el estado de un sistema mecánico en términos de variables posición y momento, y es la base para la reformulación de la mecánica clásica conocida como mecánica hamiltoniana. En mecánica cuántica, el operador Hamiltoniano es el correspondiente al observable "energía".
Producto destacado
Descripción cuántica de un sistemaEn el formalismo de la mecánica cuántica, el estado físico del sistema puede ser caracterizado por un vector en un espacio de Hilbert de dimensión infinita (lo cual permite expresar cualquier estado físico por una secuencia contable de vectores, ponderados por sus amplitudes de probabilidades respectivas). Las magnitudes físicas observables son descritas, entonces, por operadores autoadjuntos que actúan sobre este vector (o sobre estos vectores). Los resultados posibles de una medida sobre un estado y las probabilidades con las que aparecen pueden calcularse a partir del vector que representa el estado y los vectores propios del operador autoadjunto que representa la magnitud.
Hamiltoniano cuánticoEl hamiltoniano cuántico H es el observable que representa la energía total del sistema (formalmente se define como un operador autoadjunto definido sobre un dominio denso en el espacio de Hilbert del sistema). Los posibles valores de la energía de un sistema físico vienen dados por los valores propios del operador hamiltoniano: (1) donde PropiedadesPor las propiedades de los operadores autoadjuntos:
Evolución temporalLa evolución temporal de los estados cuánticos puede obtenerse a partir del Hamiltoniano a través de la ecuación de Schrödinger. Si
donde Donde la exponencial del operador Hamiltoniano se calcula usualmente mediante serie de potencias. Se puede demostrar que es un operador unitario, y es la forma común de operador de evolución temporal o propagador. |
|
| Este articulo se basa en el articulo Hamiltoniano_(mecánica_cuántica) publicado en la enciclopedia libre de Wikipedia. El contenido está disponible bajo los términos de la Licencia de GNU Free Documentation License. Véase también en Wikipedia para obtener una lista de autores. |





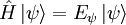
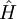 es el operador hamiltoniano,
es el operador hamiltoniano, 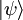 es un estado propio de
es un estado propio de 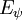 es la energía de ese estado.
es la energía de ese estado.
 , que satisfacen (
, que satisfacen (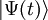 es el estado del sistema a tiempo t, tenemos:
es el estado del sistema a tiempo t, tenemos:
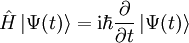 .
.
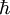 es la
es la