|
La formulación matemática rigurosa de la mecánica cuántica fue desarrollada por Paul Adrien Maurice Dirac y John von Neumann. Dicha formulación canónica se basa en un conjunto de media docena de postulados (dependiendo de la formulaciones). Este artículo presenta una enumeración más o menos canónica de dichos postulados fundamentales. Producto destacado
Postulado ITodo estado cuántico está representado por un vector normal, llamado vector de estado, en un espacio de Hilbert complejo y separable. Fijada una base de Hilbert se puede representar el estado de las siguientes formas:
Más información en: Notación bra-ket Postulado IILos observables de un sistema están representados por operadores lineales hermíticos (autoadjuntos). El conjunto de autovalores (valores propios) del observable A recibe el nombre de espectro y sus autovectores (vectores propios), exactos o aproximados, definen una base en el espacio de Hilbert.
Postulado IIICuando un sistema está en el estado
Principio de incertidumbreEl producto de las dispersiones de dos observables sobre el mismo estado está acotado. Para el caso de los observables típicos de posición (X) y momento (Px) tenemos: Esto es porque las variables X y Px son canónicas conjugadas, es decir que el conmutador Postulado IVPara cualquier estado Éste es el postulado más conflictivo de la mecánica cuántica ya que supone el colapso instantáneo de nuestro conocimiento sobre el sistema al hacer una medida filtrante. Postulado VLa evolución temporal de un sistema se rige por la ecuación de Schrödinger: Donde H es el operador de Hamilton o hamiltoniano del sistema, que corresponde a la energía del sistema. Postulado VILos operadores de posición y momento satisfacen las siguientes reglas de conmutación: Nomenclatura usada
Véase también
Categoría: Mecánica cuántica |
|
| Este articulo se basa en el articulo Formulación_matemática_de_la_mecánica_cuántica publicado en la enciclopedia libre de Wikipedia. El contenido está disponible bajo los términos de la Licencia de GNU Free Documentation License. Véase también en Wikipedia para obtener una lista de autores. |


Enciclopedia




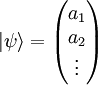
 (Donde la barra significa conjugado).
(Donde la barra significa conjugado).
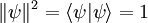 . La elección del estado normalizado no es única ya que
. La elección del estado normalizado no es única ya que 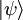 y
y 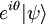 representan el mismo estado ya que la medida de cualquier magnitud en ellos es idéntica.
representan el mismo estado ya que la medida de cualquier magnitud en ellos es idéntica.
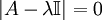

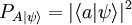 , donde
, donde 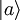 es el vector propio que representa el observable A.
es el vector propio que representa el observable A.
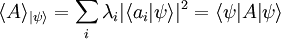
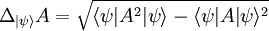
![\Delta A \Delta B \ge \frac{1}{2} \langle \psi | [A,B]| \psi \rangle](images/math/2/4/6/2466b21549649ec3e82c669833db6a3a.png)
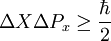
![[X,P_x]=i \hbar](images/math/d/3/b/d3b1693e6c86b1624086024ea9c6bbcf.png) .
.
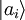 , pasa a encontrarse precisamente en ese estado
, pasa a encontrarse precisamente en ese estado 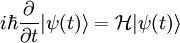
![[X_i,X_j]=0 \qquad [P_i,P_j]=0 \qquad [X_i,P_j]=i\hbar \delta_{ij}\mathbb{I}](images/math/a/5/b/a5b085c96a0cfd593cc1153bc4bd5ff8.png)
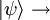 Estado cuántico
Estado cuántico 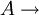
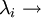 Autovalor
Autovalor 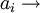 Autovector
Autovector 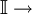 Matriz identidad
Matriz identidad 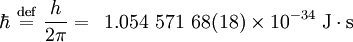 Constante reducida de Planck (h-barra)
Constante reducida de Planck (h-barra) ![[A,B] = AB - BA \rightarrow](images/math/b/8/b/b8b01dfdb1b73c80b8fa9bb1a78b1499.png) Conmutador
Conmutador

