|
En física cuántica, un observable es toda propiedad del estado de un sistema que puede ser determinada ("observada") por alguna secuencia de operaciones físicas. Estas operaciones pueden incluir, por ejemplo, el someter al sistema a diversos campos electromagnéticos y la lectura de valores en un dispositivo. Para todo observable podemos diferenciar una cualidad y una cantidad, y esta distinción resulta de especial interés en la física cuántica. Conocimientos adicionales recomendados
Observables en física clásicaEn los sistemas gobernados por la mecánica clásica, cualquier valor observable experimentalmente está relacionado por una función matemática de variables reales con el conjunto de estados posibles del sistema. En palabras llanas, podemos obtener, en sistemas muy similares, una variación continua de cantidad para cada cualidad. En mecánica clásica los observables matemáticamente son funciones de las coordenadas de posición y las velocidades (alternativamente los momentos conjugados). Debido a esto un observable en mecánica clásica puede entenderse como una función o aplicación definida sobre el espacio fásico del sistema. Gracias a esta noción, puede entenderse la relación entre los observables de la mecánica clásica y la mecánica cuántica, así el "cuadrado" de la función de onda es análogo a una distribución de probabilidad sobre el espacio fásico del sistema. La noción de observable cuántico que a primera vista parece poco intuitiva se aclara notablemente si pensamos que se corresponden intutivamente con la acción sobre distribuciones de probabilidad del espacio de fases del sistema. Mediciones de diferentes observadoresEn física clásica, pueden definirse diferentes observadores carcterizados por su posición en el espacio y el tipo de coordenadas usadas para referir las magnitudes físicas vectoriales y tensoriales. Debido a su diferente ubicación y orientación cada uno de los diferentes observadores hará medidas diferentes del mismo fenómeno. Sin embargo, la objetividad de la realidad física, conlleva que dichas medidas deben ser relacionables, mediante leyes de transformación bien definidas. En mecánica clásica no-relativista dichas transformaciones de coordenadas que relacionan las medidas de diferentes observadores vienen dadas por el grupo de Galileo, mientras que en mecánica relativista vienen dadas por el grupo de Poincaré (grupo de Lorentz ampliado con los desplazamientos). Observables en física cuánticaEn mecánica cuántica, en cambio, la relación entre los estados de un sistema y los valores de un observable es más sutil, y precisa de algo de álgebra lineal para su explicación. En la formulación matemática de la mecánica cuántica, los estados son vectores no nulos en un espacio de Hilbert V (en el que se considera que dos vectores especifican el mismo estado si y solo si son múltiplos escalares entre sí). Matemáticamente los observables en mecánica cuántica se representan por operadores lineales autoadjuntos en V. Concretamente, los operadores corresponden a la cualidad del observable, mientras que los valores propios, que forman el espectro de cada operador corresponden a los valores posibles de una medición de esa cualidad.[1] En la mecánica cuántica, los procesos de medida conllevan fenómenos que contradicen la intuición habitual, basada en los procesos de la mecánica clásica. Esto lleva ocasionalmente a equívocos sobre la propia naturaleza de la mecánica cuántica. Específicamente, si un sistema está en un estado descrito por una función de ondas, el proceso de medición afecta al estado de forma no-determinista, pero tratable estadísticamente. En particular, tras una medida, la descripción del estado del sistema por una única función de ondas puede destruirse y quedar reemplazado por un conjunto estadístico de funciones. La naturaleza irreversible de las operaciones de medida en física cuántica es llamado a veces problema de la medida o problema del colapso de la función de onda. La descripción de una medida es equivalente, desde el punto de vista matemático, a la ofrecida por la interpretación de estados relativos, en la que el sistema original se ve como un subsistema de uno mayor, y el estado del sistema original se ve como la traza parcial del estado de ese sistema mayor. Momento linealConsideremos el espacio de Hilbert de una partícula libre El espectro de este operador es puramente continuo y coincide con el eje real. Para ver esto basta considerar los vectores aproximadamente propios normalizados dados por: PosiciónEn el mismo espacio de Hilbert anterior podemos considerar el llamado operador posición (respecto a un sistema de ejes cartesianos) que da los posibles valores de ubicación de una partícula. La naturaleza supuestamente continua del espacio en mecánica cuántica convencional lleva a que dicho operador puede asumir cualquier valor real y por tanto a tener un espectro continuo. Empecemos con la definición de dicho operador autoadjunto y de su dominio: Puede verse que al igual que el operador momento, su espectro es puramente continuo y coincide con el eje real, es decir, es posible encontrar una partícula libre en cualquier posición del espacio. Esto puede verse usando la sucesión de funciones: Donde Energía (hamiltoniano)En esta sección se dan varios ejemplos de operdores hamiltonianos de sistemas físicos importantes. EspínEl observable asociado al espín es un caso de observable interesante, porque matemáticamente se realiza mediante un operador que actúa sobre un espacio de dimensión finita. Por esa razón dicho operador puede representarse por una matriz. Por ejemplo las matrices de Pauli implementan los correspondientes operadores para partículas de espín 1/2. El espacio de Hilbert de una partícula tridimensional que se mueve en un espacio tridimensional y que tiene espín n/2, se puede representar como producto tensorial de espacios de Hilbert de un espacio tipo L2 y espacio vectorial de dimensión 2n. Mediciones de diferentes observadoresLos observables con sentido físico también obedecen las leyes de transformación que relacionan observaciones hechas por distintos observadores en distintos marcos de referencia. Estas transformaciones son automorfismos del espacio de estados, esto es, transformaciones biyectivas que preservan alguna propiedad matemática. En el caso de la mecánica cuántica, los automorfismos son las transformaciones lineales unitarias o anti-unitarias del espacio de Hilbert V. En la teoría de la relatividad especial, las matemáticas de los marcos de referencia son particularmente simples, y de hecho restringen considerablemente el conjunto de observables con sentido físico. Referencias y notas
Véase también
Categoría: Mecánica cuántica |
|
| Este articulo se basa en el articulo Observable publicado en la enciclopedia libre de Wikipedia. El contenido está disponible bajo los términos de la Licencia de GNU Free Documentation License. Véase también en Wikipedia para obtener una lista de autores. |


Enciclopedia




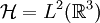 y consideremos el momento lineal (en dirección x) que viene dado por el
y consideremos el momento lineal (en dirección x) que viene dado por el 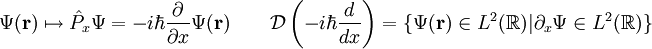
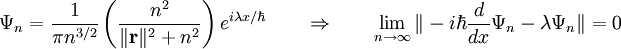
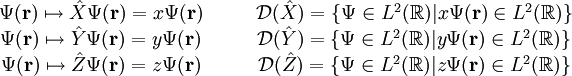
![\Psi_n = \frac{1}{\pi} \frac{(2n)^{3/2}}{[n^2\|\mathbf{r}-\mathbf{r}_0\|^2+1]^2} \qquad \Rightarrow \qquad \begin{cases} \lim_{n\to\infty} \|\hat{X}\Psi_n -x_0 \Psi_n \| = 0\\ \lim_{n\to\infty} \|\hat{Y}\Psi_n -y_0 \Psi_n \| = 0\\ \lim_{n\to\infty} \|\hat{Z}\Psi_n -z_0 \Psi_n \| = 0 \end{cases}](images/math/f/4/4/f44a2ce3e9af2328b46c8731a405ec3d.png)
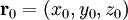 es un vector cualquiera.
es un vector cualquiera.
