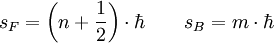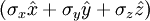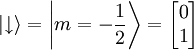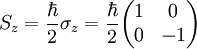|
El espín (del inglés spin 'giro, girar') se refiere a una propiedad física de las partículas subatómicas, por la cual toda partícula elemental tiene un momento angular intrínseco de valor fijo. Se trata de una propiedad intrínseca de la partícula como lo es la masa o la carga eléctrica. El espín fue introducido en 1925 por Ralph Kronig e, independientemente, por George Uhlenbeck y Samuel Goudsmit. En 1920, los químicos analíticos llegaron a la conclusión que para describir a los electrones en el átomo, además de los números cuánticos, se requería de un cuarto concepto, el llamado espín del electrón. Éste, al girar sobre su propio eje genera un campo magnético, el denominado espín. Los dos físicos, Goudsmit y Uhlenbeck, descubrieron que, si bien la teoría cuántica de la época no podía explicar algunas propiedades de los espectros atómicos, añadiendo un número cuántico adicional, el espín, se lograba dar una explicación más completa de los espectros atómicos. Pronto, el concepto de espín se amplió a todas las partículas subatómicas, incluidos los protones, los neutrones y las antipartículas. El espín proporciona una medida del momento angular y de la acción, intrínseco de toda partícula. Todo esto en contraste con la mecánica clásica, donde el momento angular se asocia a la rotación de un objeto extenso. El espín es un fenómeno exclusivamente cuántico. En las teorías cuánticas no relativistas el espín debe introducirse de manera artificial, mientras que en las relativistas aparece de manera natural.
Producto destacado
Propiedades del espínComo propiedad mecanocuántica, el espín presenta una serie de cualidades que lo distinguen del momento angular clásico:
Teorema espín-estadísticaOtra propiedad fundamental de las partículas cuánticas es que parecen existir sólo dos tipos llamados fermiones y bosones, los primeros obedecen la estadística de Fermi-Dirac y los segundos la estadística de Bose-Einstein. Eso implica que los agregados de fermiones idénticos están descritos por funciones de onda totalmente antisimétricas mientras que los bosones idénticos vienen descritos por funciones de onda totalmente simétricas. Curiosamente existe una conexión entre el tipo de estadística que obedecen las partículas y el su spin. Los fermiones tienen espines "semienteros" y los bosones enteros:
Donde n y m son números enteros positivos que dependen del tipo de partículas. Los electrones, neutrones y protones son fermiones de espín Tratamiento matemático del espínEn mecánica cuántica el espín (de una partícula de espín s) se representa como un operador sobre un espacio de Hilbert de dimensión finita de dimensión 2s+1. Este operador vectorial viene dado por: siendo σi las matrices de Pauli (o alguna otra base que genere el álgebra de Lie su(2)). El proceso de medición del espín de un electrón en la dirección z (en coordenadas cartesianas) hay dos autoestados de S. Se asignan vectores a los espines como sigue: entonces el operador correspondiente en dicha representación será Para partículas de espín superior la forma concreta de las matrices cambia. Así para partículas de espín s las matrices que representan matemáticamente el espín son matrices cuadradas de 2s+1 x 2s+1. Espín y momento magnéticoLas partículas con espín presentan un momento magnético, recordando a un cuerpo cargado eléctricamente en rotación (de ahí el origen del término: spin, en inglés, significa "girar"). La analogía se pierde al ver que el momento magnético de espín existe para partículas sin carga, como el fotón. El ferromagnetismo surge del alineamiento de los espines (y, ocasionalmente, de los momentos magnéticos orbitales) en un sólido. Aplicaciones a las nuevas tecnologías o a tecnologías futurasMagnetorresistencia y láserActualmente, la microelectrónica encuentra aplicaciones a ciertas propiedades o efectos derivados de la naturaleza del espín, como es el caso de la magnetorresistencia (MR) o la magnetorresistencia gigante (MRG) que se aprovecha en los discos duros. Se puede ver el funcionamiento de los láseres como otra aplicación de las propiedades del spin. En el caso de los bosones se puede forzar a un sistema de bosones a posicionarse en el mismo estado cuántico. Este es el principio fundamental del funcionamiento de un láser en el que los fotones, partículas de espín entero, se disponen en el mismo estado cuántico produciendo trenes de onda en fase. Espintrónica y computación cuánticaAl uso, presente y futuro, de tecnología que aprovecha propiedades específicas de los spines o que busca la manipulación de espines individuales para ir más allá de las actuales capacidades de la electrónica se la conoce como espintrónica. También se baraja la posibilidad de aprovechar las propiedades del espín para futuras computadoras cuánticas, en los que el espín de un sistema aislado pueda servir como qubit o bit cuántico. Véase también
Enlaces externos
|
|
| Este articulo se basa en el articulo Espín publicado en la enciclopedia libre de Wikipedia. El contenido está disponible bajo los términos de la Licencia de GNU Free Documentation License. Véase también en Wikipedia para obtener una lista de autores. |





 (donde
(donde 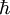 es la
es la 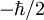 .
.
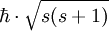 , siendo
, siendo 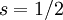 . Esto contrasta con el caso clásico donde el momento angular de un cuerpo alrededor de su eje puede asumir diferentes valores según la rotación sea más rápida o menos.
. Esto contrasta con el caso clásico donde el momento angular de un cuerpo alrededor de su eje puede asumir diferentes valores según la rotación sea más rápida o menos.