|
En física, el momento magnético de un elemento puntual es un vector que, en presencia de un campo magnético (inherentemente vectorial), se relaciona con el torque de alineación de ambos vectores en el punto en el que se sitúa el elemento . El vector de campo magnético a utilizarse es el B denominado como Inducción Magnética o Densidad de Flujo Magnético cuya magnitud es el Weber por metro cuadrado. Producto destacado
Relaciones físicasLa relación es: donde Uno de los ejemplos más simples de momento magnético es el de una espira conductora de la electricidad, con intensidad I y área A, para el cual la magnitud es: Momento magnético de espínLos electrones y muchos núcleos atómicos también tienen momentos magnéticos intrínsecos, cuya explicación requiera tratamiento mecanocuántico y que se relaciona con el momento angular de las partículas. Son estos momentos magnéticos intrínsecos los que dan lugar a efectos macroscópicos de magnetismo, y a otros fenómenos como la resonancia magnética nuclear. El momento magnético de espín es una propiedad intrínseca o fundamental de las partículas, como la masa o la carga eléctrica. Este momento está relacionado con el hecho de que las partículas elementales tienen momento angular intrínseco o espín, para partículas cargadas eso lleva inevitablemente a que se comporten de modo similar a un pequeño circuito con cargas en movimiento. Sin embargo, también existe partículas neutras sin carga eléctrica como el neutrón que no poseen que sin embargo tienen momento magnético (de hecho el neutrón no se considera realmente elemental sino formado por tres quarks cargados).
Momento magnético del electrónEl momento (dipolar) magnético de un electrón es: donde
Momento magnético orbitalCiertas disposiciones orbitales, con degeneración triple o superior, implican un momento magnético adicional, por el movimiento de los electrones como partículas cargadas. La situación es análoga a la de la espira conductora presentada arriba, pero exige un tratamiento cuántico. Los compuestos de los diferentes metales de transición presentan muy diversos momentos magnéticos, pero es posible encontrar un intervalo típico para cada metal en cada estado de oxidación, teniendo en cuenta, por supuesto, si es de espín alto o bajo.
Véase tambiénCategoría: Magnetoquímica |
||||||||||||||||||||||||||||||||||
| Este articulo se basa en el articulo Momento_magnético publicado en la enciclopedia libre de Wikipedia. El contenido está disponible bajo los términos de la Licencia de GNU Free Documentation License. Véase también en Wikipedia para obtener una lista de autores. |





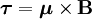
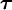 es el torque,
es el torque, 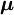 es el momento magnético, y
es el momento magnético, y 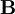 es el campo magnético. El alineamiento del momento magnético con el campo crea una diferencia en la energía potencial U:
es el campo magnético. El alineamiento del momento magnético con el campo crea una diferencia en la energía potencial U:
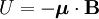
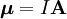
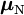
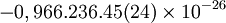
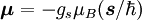
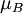 es el
es el 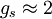 [la teoría clásica predice que
[la teoría clásica predice que 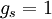 ; un gran éxito de la
; un gran éxito de la 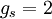 , que está muy cerca del valor exacto (que es ligeramente superior a dos; esta última corrección se debe a los efectos cuánticos del campo electromagnético)].
, que está muy cerca del valor exacto (que es ligeramente superior a dos; esta última corrección se debe a los efectos cuánticos del campo electromagnético)].


