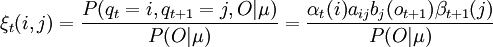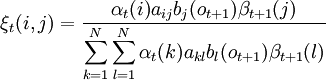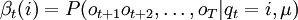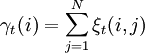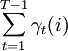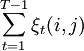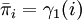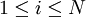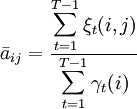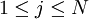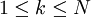Introducción
Uno de los problemas relacionado con los Modelos Ocultos de Markov (MOM) es el de encontrar un modelo μ que maximice la probabilidad de una secuencia de observaciones 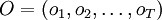 , es decir, determinar el modelo que mejor explica tal secuencia.
El problema es que no es posible encontrar tal modelo analíticamente y por ello es necesario un algoritmo iterativo como el de Baum y Welch, que permite estimar los parámetros de un modelo que hacen máxima la probabilidad de una secuencia de observables. , es decir, determinar el modelo que mejor explica tal secuencia.
El problema es que no es posible encontrar tal modelo analíticamente y por ello es necesario un algoritmo iterativo como el de Baum y Welch, que permite estimar los parámetros de un modelo que hacen máxima la probabilidad de una secuencia de observables.
El algoritmo de Baum y Welch
Dada una secuencia de observaciones 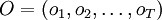 , el algoritmo de Baum y Welch permite estimar los parámetros de un Modelo oculto de Markov (MOM) μ que maximizan la probabilidad de dicha secuencia, es decir, P(O | μ). , el algoritmo de Baum y Welch permite estimar los parámetros de un Modelo oculto de Markov (MOM) μ que maximizan la probabilidad de dicha secuencia, es decir, P(O | μ).
Valores esperados
Antes de describir el proceso de estimación, necesitamos conocer:
- el número esperado de transiciones desde el estado i en O y
- el número esperado de transiciones desde el estado i al estado j en O
Para ello definimos previamente ξt(i,j) como la probabilidad de estar en el estado i en el instante t y en el estado j en el instante t + 1, dado una observación O y el modelo μ.
ξt(i,j) = P(qt = i,qt + 1 = j | O,μ)
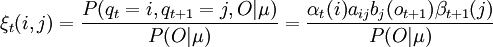
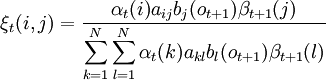
donde los valores αt(i) y βt(i) se pueden calcular eficientemente con el algoritmo de avance-retroceso.

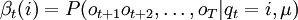
La figura muestra un esquema parcial de los elementos necesarios para el cálculo de ξ(i,j).
Definimos también γt(i) como la probabilidad de estar en el estado i en el instante t,
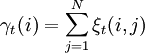
Sumando cada γt(i) en cada instante de tiempo, obtenemos:
- el número esperado de transiciones desde el estado i en la observación O
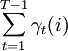
y haciendo lo mismo con cada ξt(i,j), obtenemos:
- el número esperado de transiciones desde el estado i al estado j en la observación O
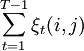
Reestimación
El funcionamiento del procedimiento iterativo es básicamente el siguiente:
- Se parte de un modelo inicial que se puede seleccionar aleatoriamente.
- Se realiza el cálculo de las transiciones y símbolos de emisión que son más probables según el modelo inicial escogido.
- Se construye un nuevo modelo en el que se incrementa la probabilidad de las transiciones y símbolos determinados en el paso anterior. Para la secuencia de observables en cuestión, el modelo tendrá ahora una probabilidad mayor que el modelo anterior.
Este proceso de entrenamiento se repite varias veces hasta que no exista mejora entre un modelo y el siguiente revisado.
Probabilidad de estar en el estado i en el instante de tiempo t = 1:
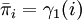
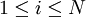
Número esperado de transiciones de i a j / número esperado de transiciones desde i:
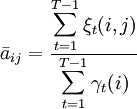
 , , 
Número esperado de veces que se pasa por el estado j y se observa ok / número esperado de veces que se pasa por el estado j:

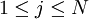 , , 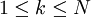
Otras preguntas fundamentales
Otros dos problemas que es importante saber resolver para utilizar los MOO son:
- ¿Cuál es la secuencia óptima S de estados, dada una secuencia de observaciones O? (algoritmo de Viterbi)
- ¿Cuál es la probabilidad de una secuencia de observaciones
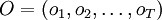 dado un modelo μ = (π,A,B)? Es decir, ¿cómo podemos calcular de forma eficiente P(O | μ)? (cálculo hacia adelante y hacia atrás). dado un modelo μ = (π,A,B)? Es decir, ¿cómo podemos calcular de forma eficiente P(O | μ)? (cálculo hacia adelante y hacia atrás).
Véase también
|




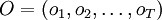 , es decir, determinar el modelo que mejor explica tal secuencia.
El problema es que no es posible encontrar tal modelo analíticamente y por ello es necesario un algoritmo iterativo como el de Baum y Welch, que permite estimar los parámetros de un modelo que hacen máxima la probabilidad de una secuencia de observables.
, es decir, determinar el modelo que mejor explica tal secuencia.
El problema es que no es posible encontrar tal modelo analíticamente y por ello es necesario un algoritmo iterativo como el de Baum y Welch, que permite estimar los parámetros de un modelo que hacen máxima la probabilidad de una secuencia de observables.