|
Un modelo oculto de Markov o HMM (por sus siglas del inglés, Hidden Markov Model) es un modelo estadístico en el que se asume que el sistema a modelar es un proceso de Markov de parámetros desconocidos. El objetivo es determinar los parámetros desconocidos (u ocultos, de ahí el nombre) de dicha cadena a partir de los parámetros observables. Los parámetros extraídos se pueden emplear para llevar a cabo sucesivos análisis, por ejemplo en aplicaciones de reconocimiento de patrones. Un HMM se puede considerar como la red bayesiana dinámica más simple. En un modelo de Markov normal, el estado es visible directamente para el observador, por lo que las probabilidades de transición entre estados son los únicos parámetros. En un modelo oculto de Markov, el estado no es visible directamente, sino que sólo lo son las variables influídas por el estado. Cada estado tiene una distribución de probabilidad sobre los posibles símbolos de salida. Consecuentemente, la secuencia de símbolos generada por un HMM proporciona cierta información acerca de la secuencia de estados. Los modelos ocultos de Markov son especialmente aplicados a reconocimiento de formas temporales, como reconocimiento del habla, de escritura manual, de gestos o bioinformática. Producto destacado
HistoriaLos modelos ocultos de Markov fueron descritos por primera vez en una serie de artículos estadísticos por Leonard E. Baum y otros autores en la segunda mitad de la década de 1960. Una de las primeras aplicaciones de HMMs fue reconocimiento del habla, comenzando en la mitad de la década de 1970.[1] En la segunda mitad de la década de 1980, los HMMs comenzaron a ser aplicados al análisis de secuencias biológicas, en particular de DNA. Desde entonces, se han hecho ubicuos en el campo de la bioinformática.[2] Arquitectura de un modelo oculto de MarkovEl diagrama que se encuentra más abajo muestra la arquitectura general de un HMM. Cada óvalo representa una variable aleatoria que puede tomar determinados valores. La variable aleatoria x(t) es el valor de la variable oculta en el instante de tiempo t. La variable aleatoria y(t) es el valor de la variable observada en el mismo instante de tiempo t. Las flechas indican dependencias condicionales. Del diagrama queda claro que el valor de la variable oculta x(t) (en el instante t) solo depende del valor de la variable oculta x(t − 1) (en el instante t − 1). A esto se lo llama la propiedad de Markov. De forma similar, el valor de la variable observada y(t) solo depende del valor de la variable oculta x(t) (ambas en el instante t). Probabilidad de una secuencia observadaLa probabilidad de observar la secuencia donde la sumatoria se extiende sobre todas las secuencias de nodos ocultos Definición formal de un Modelo Oculto de MarkovUna notación habitual de un MOM es la representación como una tupla (Q,V,π,A,B):
La secuencia de observables se denota como un conjunto
Uso de modelos ocultos de MarkovExisten tres problemas canónicos asociados con HMMs:
EjemploImagínese que tiene un amigo que vive lejos y con quien habla a diario por teléfono acerca de lo que hizo durante el día. A su amigo le interesan tres actividades: caminar por la plaza, salir de compras y limpiar su departamento. Lo que su amigo hace depende exclusivamente del estado del tiempo en ese día. Usted no tiene información clara acerca del estado del tiempo donde su amigo vive, pero conoce tendencias generales. Basándose en lo que su amigo le dice que hizo en el día, usted intenta adivinar el estado del tiempo. Supóngase que el estado del tiempo se comporta como una cadena de Markov discreta. Existen dos estados, "Lluvioso" y "Soleado", pero usted no los puede observar directamente, es decir, están ocultos. Existe también una cierta posibilidad de que su amigo haga una de sus actividades cada día, dependiendo del estado del tiempo: "caminar", "comprar" o "limpiar". Dado que su amigo le cuenta sus actividades del día, esas son las observaciones. El sistema completo es un modelo oculto de Markov. Usted conoce las tendencias generales del tiempo en el área y lo que a su amigo le gusta hacer. En otras palabras, los parámetros del HMM son conocidos. Pueden escribirse usando el lenguaje de programación Python: observaciones = ('caminar', 'comprar', 'limpiar') probabilidad_inicial = {'Lluvioso': 0.6, 'Soleado': 0.4} probabilidad_transicion = { 'Lluvioso' : {'Lluvioso': 0.7, 'Soleado': 0.3},
'Soleado' : {'Lluvioso': 0.4, 'Soleado': 0.6},
}
probabilidad_emision = { 'Lluvioso' : {'caminar': 0.1, 'comprar': 0.4, 'limpiar': 0.5},
'Soleado' : {'caminar': 0.6, 'comprar': 0.3, 'limpiar': 0.1},
}
En esta porción de código, Aplicaciones de modelos ocultos de Markov
NotasVéase también
Enlaces externos
Categoría: Bioinformática |
|
| Este articulo se basa en el articulo Modelo_oculto_de_Markov publicado en la enciclopedia libre de Wikipedia. El contenido está disponible bajo los términos de la Licencia de GNU Free Documentation License. Véase también en Wikipedia para obtener una lista de autores. |





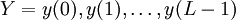 de longitud
de longitud 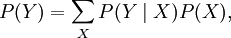
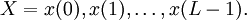 El cálculo por fuerza bruta de
El cálculo por fuerza bruta de 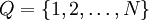 . El estado inicial se denota como
. El estado inicial se denota como 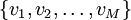 observables en cada estado.
observables en cada estado. 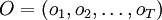 .
.


