|
la constante de equilibrio puede ser definida como donde {A} es la actividad (cantidad adimensional) de la sustancia química A y así sucesivamente. Es solo una convención el poner las actividades de los productos como numerador y de los reactantes como denominadores. Para el equilibrio en los gases, la actividad de un componente gaseoso es el producto de los componentes de la presión parcial y del coeficiente de fugacidad. Para el equilibrio en una solución, la actividad es el producto de la concentración y el coeficiente de actividad. Es una practica común el determinar las constantes de equilibrio en un medio de fuerzas iónicas altas. Bajo esas circunstancias, el cociente de los coeficientes de actividad son constantes efectivamente y la constante de equilibrio es tomada para ser un cociente de concentración. Todas las constantes de equilibrio dependen de la temperatura y la presión (o el volumen). El conocimiento de las constantes de equilibrio es esencial para el entendimiento de muchos procesos naturales como la transportación de oxigeno por la hemoglobina en la sangre o la homeostasis ácido-base en el cuerpo humano. Las constantes de estabilidad, constantes de formación, constantes de enlace, constantes de asociación y disociación son todos tipos de constantes de equilibrio. Conocimientos adicionales recomendados
Tipos de constantes de equilibrioConstantes de asociación y disociaciónEn la química orgánica y en la bioquímica se acostumbra a usar el valor pKa para el equilibrio de disociación. donde Kdis es un constante de disociación de los ácidos. Para bases, la constante de disociación es pKb. Se relacionan mediante la ecuación:
Por otro lado las constantes de estabilidad para complejos metálicos y las constantes de enlace para complejos mas grandes son generalmente expresadas como constantes de asociación. Si consideramos el equilibrio como se acostumbra a usar constantes de asociación para ML y HL.
Constantes de BrønstedEl pH esta definido en términos de la actividad de los iones de hidrógeno Si, al determinar la constante de equilibrio, el pH es medido por significado de un electrodo de vidrio, una constante de equilibrio mezclada, también conocida como la constante de Brønsted, que puede resultar Todo esto depende de como el electrodo esta calibrado en referencia a las soluciones de actividad conocida o concentración conocida. En ultimo de los casos, la constante de equilibrio podría ser un cociente de concentración. Si el electrodo esta calibrado en términos de concentración de iones hidrógeno conocidas, podría ser mejor escribir p[H] en vez de pH, pero esto no se ha adoptado del todo. Constantes de HidrólisisEn una solución acuosa, la concentración de los iones hidroxilos esta relacionada a la concentración de los iones hidrógeno así: El primer paso en la hidrólisis de los iones metálicos[2] puede ser expresado de dos maneras diferentes Obtenemos que β * = KKW. Las constantes de hidrólisis son usualmente reportadas en la forma β * y eso conduce a la aparición de los valores extraños. Por ejemplo, si lgK=4 y lg KW=-14, lg β * = 4 -14 = -10. En general cuando el producto de la hidrólisis contiene n grupos hidróxidos lg β * = lg K + n lg KW.
Dependencia de la temperaturamuestra que cuando una reacción exotérmica (ΔH
La constante de equilibrio es asociada al cambio en la energía de Gibbs estándar de una reacción así donde ΔG Si la constante de equilibrio ha sido determinada y la entalpía de la reacción estándar ha sido también determinada, por un calorímetro por ejemplo, esta ecuación permite el cambio en la entropía estándar para la reacción realizada. Una formulación más complejaLos cálculos de KT2 de la KT1 conocida puede ser propuesta como sigue si las propiedades termodinámicas estándar están disponibles. El efecto de la temperatura en constante equilibrio es equivalente al efecto de la temperatura en la energía de Gibbs ya que: donde Aquí el término estándar denota el comportamiento ideal y una concentración hipotética estándar de 1 mol/kg. Esto no implica que cualquier otra temperatura o presión de sea mas conveniente al describir sistemas acuosos que a otros rangos de temperatura o presión.[3] La energía estándar de Gibbs (de cada especie o de toda la reacción) puede ser representada (de la definición de base) así:
En esta ecuación, los efectos de la temperatura en la energía de Gibbs (y así de la constante de equilibrio) es descrita enteramente por la capacidad calorífica. Para evaluar las integrales en esta ecuación, la forma de la dependencia de la capacidad calorífica en la temperatura necesita ser conocida. Ahora, si se expresa la capacidad calorífica estándar
entonces las integrales pueden evaluarse y la siguiente forma es obtenida finalmente: Todas las constantes y la entropía absoluta, Dependencia de presiónLa dependencia de presión de la constante de equilibrio es usualmente débil en el rango de presiones que normalmente se encuentra en la industria y por lo tanto se lo rechaza usualmente en la practica. Esto es verdadero para reactivos o productos condensados o gaseosos.
Recursos de datos
Véase tambiénReferencias
Enlaces externos
|
|
| Este articulo se basa en el articulo Constante_de_equilibrio publicado en la enciclopedia libre de Wikipedia. El contenido está disponible bajo los términos de la Licencia de GNU Free Documentation License. Véase también en Wikipedia para obtener una lista de autores. |


Enciclopedia

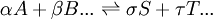
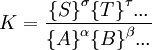
![K_c=\frac{{[S]} ^\sigma {[T]}^\tau ... } {{[A]}^\alpha {[B]}^\beta ...}](images/math/2/b/1/2b116a1f13940176246dd9e08a0c0be3.png)



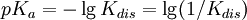
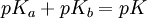 .
.
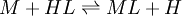
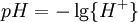
![HL \rightleftharpoons L+H:pK =-\lg \left(\frac{[L]\{H\}}{[HL]} \right)](images/math/e/5/d/e5d922145e1a8def4bdf66cb78305d7c.png)
![K_W=[H][OH]: [OH]=K_W[H]^{-1}\,](images/math/0/6/3/06395af2bb950df6fb44453943fb9d6b.png)
![M(H_2O) \rightleftharpoons M(OH) +H:[M(OH)]=\beta^*[M][H]^{-1}](images/math/7/b/5/7b509a36a1d72e0a432997985836e938.png)
![M+OH \rightleftharpoons M(OH):[M(OH)]=K[M][OH]=K K_W[M][H]^{-1}](images/math/4/f/d/4fdce4f0a46e9cd8572940763f7ea439.png)
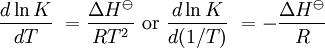
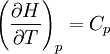 donde Cp es la
donde Cp es la 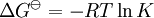
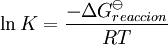
 es la energía de la reacción estándar de Gibbs que es la suma de las energías estándar de Gibbs de los productos de la reacción menos la suma de las energías de los resultantes.
es la energía de la reacción estándar de Gibbs que es la suma de las energías estándar de Gibbs de los productos de la reacción menos la suma de las energías de los resultantes.
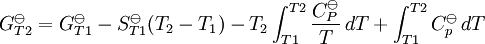
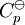 como una función de temperatura absoluta usando correlaciones en una de las siguientes formas:
como una función de temperatura absoluta usando correlaciones en una de las siguientes formas: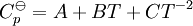
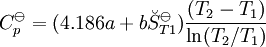
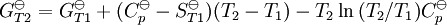
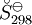 , requieren de la evaluación de
, requieren de la evaluación de 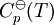 , como los valores de G298 K y S298 K para muchas especies que se encuentran fácilmente en los libros sobre el tema.
, como los valores de G298 K y S298 K para muchas especies que se encuentran fácilmente en los libros sobre el tema.
