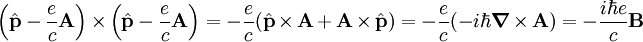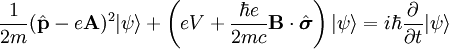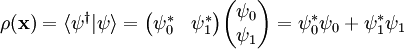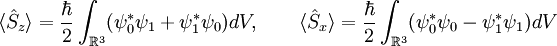|
La ecuación de Pauli o ecuación de Schrödinger-Pauli, es una generalización o reformulzación de la ecuación de Schrödinger para partículas de espín 1/2 que tiene en cuenta la interacción entre el espín y el campo electromagnético. Esta ecuación es el límite no relativista de la ecuación de Dirac y puede usarse para describir electrones que para los cuales los efectos relativistas de la velocidad pueden despreciarse. La ecuación de Pauli fue propuesta originalmente por Wolfgang Pauli. Producto destacado
Forma de la ecuaciónLa ecuación de Pauli tiene la forma: (1) Donde:
Forma alternativaSi se usan la propiedades de las matrices de Pauli se demuestra fácilmente la siguiente igualdad:[1] Y como: La ecuación () puede reescribirse en la forma: (2) Derivación históricaLa derivación histórica de la ecuación se hizo siguiendo principios formales no muy diferentes del principio de acoplamiento mínimo usado posteriormente en la teoría cuántica de campos. Densidad de probabilidadLa ecuación de Pauli para el espinor de Pauli formado por dos componentes, cada uno con un significado similar a la función de onda. De hecho, en ausencia de campo la ecuación de Pauli se reduce a una ecuación de Schrödinger "doble", es decir, cada cada una de las dos componentes del espinor satisface independiente la ecuación de Schrödinger. La densidad de probabilidad conjunta viene dada por las reglas usuales de la mecánica cuántica: E igualmente puede probarse que el valor esperado para los operadores de espín viene dado: Referencia
Categoría: Mecánica cuántica |
|
| Este articulo se basa en el articulo Ecuación_de_Schrödinger-Pauli publicado en la enciclopedia libre de Wikipedia. El contenido está disponible bajo los términos de la Licencia de GNU Free Documentation License. Véase también en Wikipedia para obtener una lista de autores. |



![\left[ \frac{1}{2m}(\hat\boldsymbol{\sigma}\cdot(\hat\mathbf{p} - e \mathbf{A}))^2 + eV \right] |\psi\rangle = i \hbar \frac{\part}{\part t} |\psi\rangle](images/math/8/0/3/803cc11f8b0d78f9940d46d95e2bddc5.png)
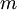 es la masa de la partícula.
es la masa de la partícula.
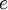 es la carga eléctrica de la partícula.
es la carga eléctrica de la partícula.
 es un "vector" cuyas tres componentes son precisamente las
es un "vector" cuyas tres componentes son precisamente las 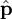 es el operador vectorial asociado al momento lineal. Las componentes de este vector son
es el operador vectorial asociado al momento lineal. Las componentes de este vector son 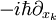
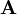 es el potencial vector del campo electromagnético.
es el potencial vector del campo electromagnético.
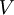 es el potencial eléctrico escalar.
es el potencial eléctrico escalar.
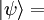 es un espinor formado por dos
es un espinor formado por dos 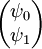 .
.
![\left[ \hat\boldsymbol{\sigma} \cdot \left( \hat\mathbf{p} -\frac{e}{c} \mathbf{A} \right)\right]^2 = \left( \hat\mathbf{p} -\frac{e}{c} \mathbf{A} \right)^2 + i \hat\boldsymbol{\sigma} \cdot \left( \hat\mathbf{p} -\frac{e}{c} \mathbf{A} \right) \times \left( \hat\mathbf{p} -\frac{e}{c} \mathbf{A} \right)](images/math/b/c/5/bc52aed39551ce2472c4df6d19ed6657.png)