|
Producto destacadoEn mecánica cuántica, la esfera de Bloch es una representación geométrica del espacio de estados de un sistema cuántico de dos niveles. Su nombre alude al físico suizo Felix Bloch. Geométricamente se trata de una esfera de radio unidad en que cada punto de la superficie corresponde unívocamente a un estado puro del espacio de Hilbert bidimensional, que caracteriza a un sistema cuántico de dos niveles. Cada par de puntos diametralmente opuestos sobre la esfera de Bloch corresponde a dos estados ortonormales en el espacio de Hilbert, que forman una base del mismo. Tales estados resultan ser autovectores de la proyección del operador de espín 1/2 sobre la dirección que determinan los dos puntos. Dicho operador se expresa empleando las matrices de Pauli, y todo sistema cuántico de dos niveles puede equipararse al caso de espín 1/2. El punto de coordenadas cartesianas (0,0,1) corresponde al autovector con autovalor positivo de la matriz de Pauli σz, mientras que el punto opuesto (0,0,-1) corresponde al autovector con autovalor negativo. En la terminología de computación cuántica, empleada al tratar los qubits, ambos estados se designan por Lo dicho para los puntos sobre el eje Z vale para los otros ejes empleando en cada caso la matriz de Pauli correspondiente.
El qubitPara mostrar explícitamente dicha correspondencia, considérese la descripción de la esfera de Bloch en términos de un qubit. El estado general del mismo, con Obsérvese que el ángulo polar, de un punto de la esfera respecto al sentido positivo del eje Z, es 2θ. La correspondencia entre puntos de la esfera y estados es unívoca siempre, pero la parametrización de los puntos antipodales sobre el eje Z deja de ser única empleando coordenadas esféricas, algo relacionado con las propiedades topológicas de la esfera en el espacio euclideo tridimensional. Ayuda visualUno de los usos de la esfera de Bloch es el de visualizar la acción de diferentes puertas lógicas en computación cuántica, o la evolución temporal del estado de un sistema de dos niveles descrito por un hamiltoniano, como al estudiar los pulsos empleados en resonancia magnética nuclear. En ambos casos se debe estudiar la acción de una matriz unitaria 2x2, que siempre se puede descomponer como producto de operadores de rotación. Un operador de rotación se define por un eje y un ángulo de giro. La acción de un operador de rotación sobre el estado cuántico se traduce, en lo que se refiere al punto asociado al estado sobre la esfera de Bloch, en una rotación del punto respecto al eje de rotación en el ángulo de giro. Por ejemplo la puerta lógica cuántica que realiza la transformación de Hadamard, se describe por la matriz Sobre la esfera de Bloch la transformación de Hadamard equivale a una rotación de 90º en torno al eje Y, seguida de una rotación de 180º respecto al eje X. O también, de forma equivalente, a una rotación de 180º respecto al eje Z seguida de una rotación de 90º respecto al eje Y. Así puede comprobarse visualmente que la transformación de Hadamard lleva el punto de coordenadas cartesianas (1,0,0) al punto (0,0,1), lo que corresponde a la expresión analítica
Categoría: Mecánica cuántica |
| Este articulo se basa en el articulo Esfera_de_Bloch publicado en la enciclopedia libre de Wikipedia. El contenido está disponible bajo los términos de la Licencia de GNU Free Documentation License. Véase también en Wikipedia para obtener una lista de autores. |




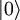 y
y 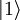 respectivamente. Estos estados en terminología de
respectivamente. Estos estados en terminología de 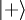 y
y 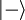 , o “espín arriba” y “espín abajo”.
, o “espín arriba” y “espín abajo”.
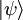 , puede escribirse como una superposición de los vectores ket
, puede escribirse como una superposición de los vectores ket 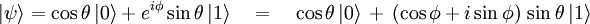
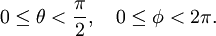
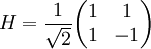
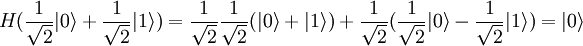 .
.


