|
La notación cor-chete (también conocida como la notación bra-ket, o notación de Dirac por su inventor Paul Dirac) es la notación estándar para describir los estados cuánticos en la teoría de la mecánica cuántica. Puede también ser utilizada para denotar vectores abstractos y funcionales lineales en las matemáticas puras. Es así llamada porque el producto interior de dos estados es denotado por el corchete angular (angle bracket, en inglés), Conocimientos adicionales recomendados
Cores y chetesEn mecánica cuántica, el estado de un sistema físico se identifica con un vector en el espacio de Hilbert complejo, H. Cada vector se llama un "chete", y se escribe como donde esto es una función lineal continua de H a los números complejos C, definido como
para todos los chetes Incidentemente, la notación cor-chete puede ser utilizada incluso si el espacio vectorial no es un espacio de Hilbert. En cualquier espacio de Banach B, los vectores pueden ser notados como cores y los funcionales lineales continuos por los chetes. Sobre cualquier espacio vectorial sin topología, se puede también denotar los vectores con chetes y los funcionales lineales por los cores. En estos contextos más generales, el corchete no tiene el significado de un producto interno, porque el teorema de representación de Riesz no se aplica. La aplicación del cor
En mecánica cuántica, ésta es la amplitud de probabilidad para que el estado ψ colapse en el estado φ. PropiedadesLos cores y chetes se pueden manipular de las maneras siguientes:
es dual a
Operadores linealesSi A: H → H es un operador lineal, se puede aplicar A al chete
Esta expresión se escribe comúnmente como Una manera conveniente de definir operadores lineales en H es dada por el producto exterior: si
denota un operador que mapea el chete
Cores y chetes compuestosDos espacios de Hilbert V y W pueden formar un tercer espacio Si
Las representaciones en términos de cores y chetesEn mecánica cuántica, es a menudo conveniente trabajar con las proyecciones de los vectores de estado sobre una base particular, más bien que con los vectores mismos. Este proceso es muy similiar al uso de vectores coordinados en álgebra lineal. Por ejemplo, el espacio de Hilbert de partículas puntuales de espín cero es generado por una base de posición
Es entonces usual definir operadores lineales que actúan sobre funciones de ondas en términos de operadores lineales que actúan en chetes, como
Aunque el operador A en el lado izquierdo de esta ecuación, por convención, se etiqueta de la misma manera que el operador en el lado derecho, debe considerarse que los dos son entidades conceptualmente diversas: el primero actúa sobre funciones de ondas, y el segundo actúa sobre chetes. Por ejemplo, el operador de momento p tiene la forma siguiente
Se encuentra de vez en cuando una expresión como
Esto es un abuso de notación, aunque bastante común. El operador diferencial debe ser entendido como un operador abstracto, actuando en chetes, que tiene el efecto de diferenciar funciones de ondas una vez que la expresión se proyecta en la base de posición. Para otros detalles, véase espacio equipado de Hilbert.
Véase también: Categoría: Mecánica cuántica |
|
| Este articulo se basa en el articulo Notación_cor-chete publicado en la enciclopedia libre de Wikipedia. El contenido está disponible bajo los términos de la Licencia de GNU Free Documentation License. Véase también en Wikipedia para obtener una lista de autores. |


Enciclopedia

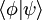 , consistiendo en una parte izquierda,
, consistiendo en una parte izquierda, 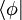 , llamada el cor, y una parte derecha,
, llamada el cor, y una parte derecha, 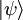 , llamada el chete.
, llamada el chete.



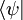
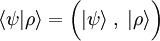 para todos los chetes
para todos los chetes 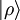
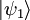 y
y 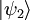 , y números complejos c1 y c2, entonces, puesto que los cores son funcionales lineales,
, y números complejos c1 y c2, entonces, puesto que los cores son funcionales lineales,
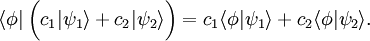
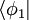 y
y 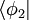 , y números complejos c1 y c2, entonces, por la definición de la adición y la multiplicación escalar de funcionales lineales,
, y números complejos c1 y c2, entonces, por la definición de la adición y la multiplicación escalar de funcionales lineales,
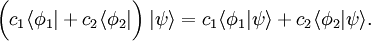
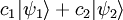
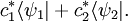
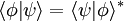 .
.
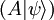 . Los operadores lineales son ubicuos en la teoría de la mecánica cuántica. Por ejemplo, se utilizan
. Los operadores lineales son ubicuos en la teoría de la mecánica cuántica. Por ejemplo, se utilizan 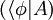 , definido como funcional lineal en H por la regla
, definido como funcional lineal en H por la regla
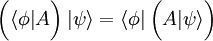 .
.
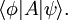
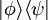
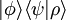 (donde
(donde 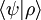 es un escalar que multiplica el vector
es un escalar que multiplica el vector 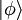 ). Una de las aplicaciones del producto externo es para construir un operador de proyección o proyector dado un chete
). Una de las aplicaciones del producto externo es para construir un operador de proyección o proyector dado un chete 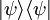
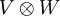 por producto tensorial. En mecánica cuántica, esto se utiliza para describir conjuntos compuestos. Si un conjunto se compone de dos subconjuntos descritos por V y W respectivamente, entonces el espacio de Hilbert del conjunto entero es el producto tensorial de los dos espacios. La excepción a esto es si los subconjuntos son realmente
por producto tensorial. En mecánica cuántica, esto se utiliza para describir conjuntos compuestos. Si un conjunto se compone de dos subconjuntos descritos por V y W respectivamente, entonces el espacio de Hilbert del conjunto entero es el producto tensorial de los dos espacios. La excepción a esto es si los subconjuntos son realmente 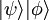 o
o 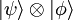 o
o 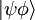 .
.
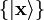 , donde el índice x se extiende sobre el conjunto de los vectores de posición. Partiendo de cualquier chete
, donde el índice x se extiende sobre el conjunto de los vectores de posición. Partiendo de cualquier chete 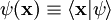 .
.
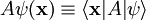 .
.
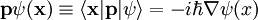 .
.
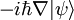 .
.
